2. Тимчасова вартість грошей

2.1 Основні поняття, пов'язані

з фінансовими операціями

Одне з найважливіших властивостей грошових потоків - їх розподіленість у часі. При аналізі щодо короткострокових періодів (до 1 року) в умовах стабільної економіки дане властивість має незначний вплив, яким часто нехтують. Визначаючи річний обсяг реалізації по підприємству, просто складають суми виручки за кожен з місяців звітного року. Аналогічно надходять із іншими грошовими потоками, що дозволяє оперувати їх підсумковими значеннями. Однак в разі більш тривалих періодів чи в умовах високої інфляції виникає серйозна проблема забезпе

печення порівнянності даних. Одна і та ж номінальна сума грошей, отримана підприємством з інтервалом в 1 рік і більше, в таких умовах отримує неоднакову цінність. Очевидно, що 1 млн. Руб. на початку 1992 р був значно вагомішим мільйона «зразка» 1993 і пізніших років. Як правило, в таких випадках проводять коригування звітних даних з урахуванням інфляції. Але проблема не зводиться тільки до обліку інфляції. Один з основоположних принципів фінансового менеджменту - визнання тимчасової цінності грошей, т. Е. Залежно їх реальної вартості від величини проміжку часу, що залишається до їх отримання або витрачання. В економічній теорії дане властивість називається позитивним тимчасовим перевагою.

Поряд з інфляційним знеціненням грошей існує ще як мінімум три найважливіші причини даного економічного феномена. По-перше, «сьогоднішні» гроші завжди цінніше «завтрашніх» через ризик неотримання останніх, і цей ризик буде тим вище, чим більше проміжок часу, що відокремлює одержувача грошей від цього «завтра». По-друге, маючи в своєму розпорядженні грошовими коштами «сьогодні», економічний суб'єкт може вкласти їх в яке-небудь прибуткове підприємство і заробити прибуток, в той час як одержувач майбутніх грошей позбавлений цієї можливості. Прощаючись із грошима «сьогодні» на певний період часу (припустимо, даючи їх в борг на 1 місяць), власник не тільки піддає себе ризику їх неповернення, але і несе реальні економічні втрати в формі неодержаних доходів від інвестування. Крім того, знижується його платоспроможність, так як будь-які зобов'язання, одержувані їм замість грошей, мають нижчу ліквідність, ніж «живі» гроші. Таким чином, зростає ризик втрати ліквідності, і це третя причина позитивного тимчасового переваги. Природно, більшість власників грошей не згодні безкоштовно приймати на себе настільки суттєві додаткові ризики. Тому при наданні кредиту встановлюють такі умови його повернення, які повинні повністю відшкодувати всі моральні і матеріальні незручності, що виникають у людини, розлучається (нехай навіть і тимчасово) з грошима.

Кількісною мірою величини цього відшкодування є процентна ставка. З її допомогою можна визначити як майбутня вартість «сьогоднішніх» грошей (наприклад, якщо їх збираються позичити), так і справжня (сучасна, поточна, або приведена) вартість «завтрашніх» грошей (наприклад, тих, якими обіцяють розплатитися через рік після поставки товарів або надання послуг). У першому випадку говорять про операції нарощення, тому майбутню вартість грошей часто називають нарощеної. У другому випадку виконується дисконтування, або приведення майбутньої вартості до її сучасною величині (поточному моменту) - звідси термін дисконтована - приведена, або поточна, вартість. Операції нарощення грошей по процентній ставці більш прості і зрозумілі, так як з ними доводиться стикатися досить часто тим, хто бере чи дає гроші в борг. Однак для фінансового менеджменту значно більше важливе значення має дисконтування грошових потоків, приведення їх майбутньої вартості до сучасного моменту часу для забезпечення порівнянності величини розподілених за часом платежів. В принципі, дисконтування - це нарощення «навпаки», однак для фінансових розрахунків важливі деталі, тому необхідно більш детально розглянути як пряму, так і зворотну задачі процентних обчислень. Перш ніж розглядати їх стосовно до грошових потоків, слід засвоїти найбільш елементарні операції з одиничними сумами (разовими платежами).

Відсоткова ставка показує ступінь інтенсивності зміни вартості грошей у часі. Абсолютна величина цієї зміни називається відсотком і вимірюється в грошових одиницях (наприклад, рублях), що позначаються I. Якщо позначити майбутню суму S, а сучасну (чи початкову) P, то
I = S - P. Процентна ставка i - відносна величина, яка вимірюється в десяткових дробах або%, вона визначається діленням відсотків на початкову суму:

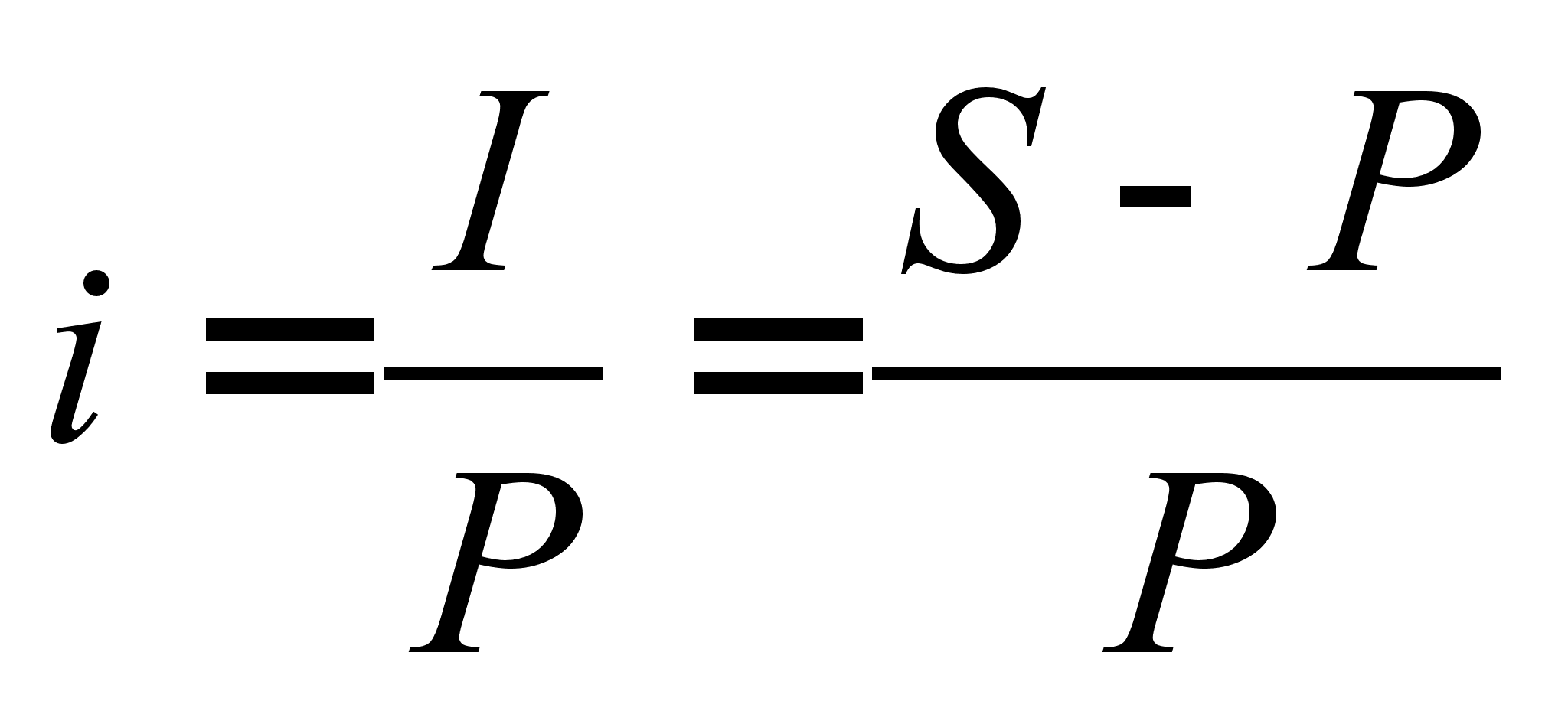. (2.1.1)

Можна помітити, що формула розрахунку процентної ставки ідентична розрахунку статистичного показника «темп приросту». Дійсно, якщо абсолютна сума відсотка (I) являє собою приріст сучасної величини, то ставлення цього приросту до найсучаснішою величині і буде темпом приросту перовначальной суми. Нарощення початкової суми по процентній ставці називається декурсівних методом нарахування відсотків.

Крім процентної існує облікова ставка d (інша назва - ставка дисконту), розмір якої визначається за формулою

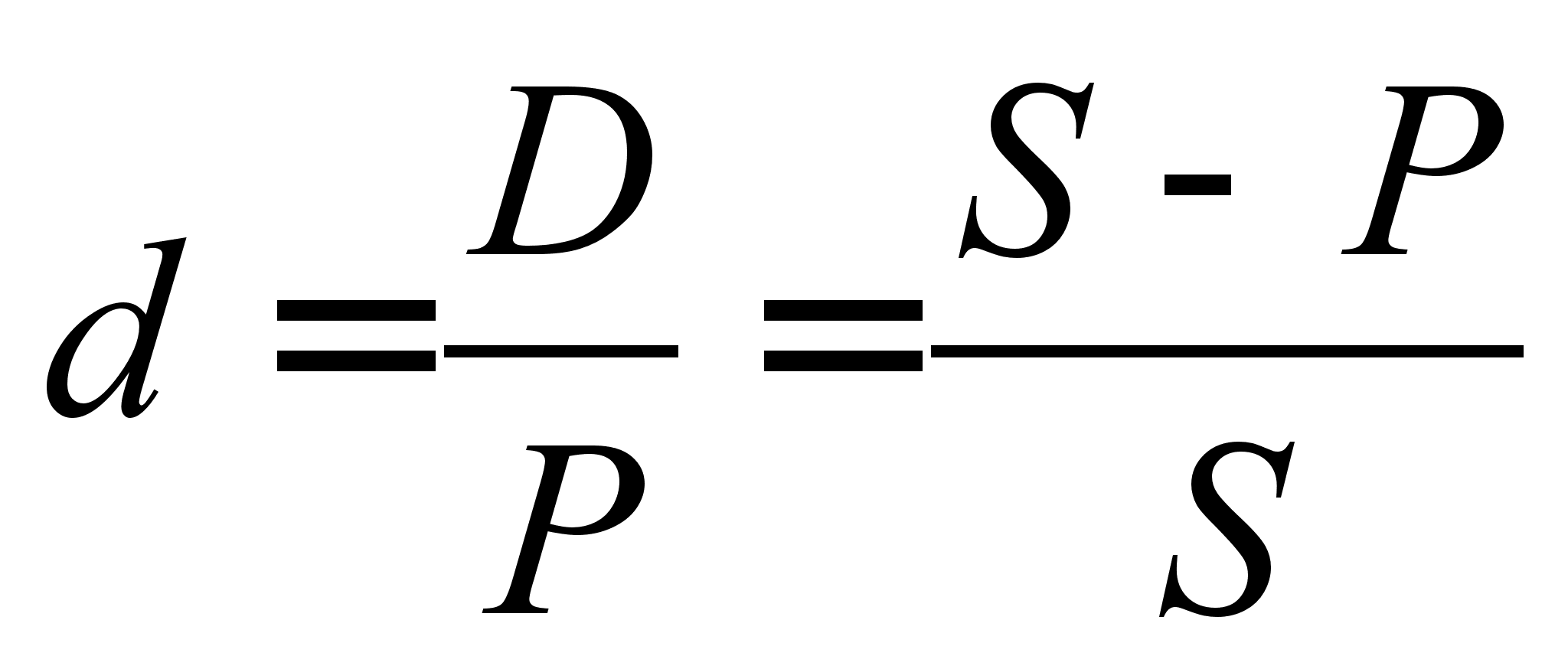, (2.1.2)

де D - сума дисконту.

Порівнюючи формули (2.1.2) і (2.1.3), можна помітити, що сума відсотків I і величина дисконту D визначаються однаковим чином - як різниця між майбутньою і сучасної вартостями. Однак зміст, вкладений в ці терміни, неоднаковий. Якщо в першому випадку мова йде про приріст поточної вартості, свого роду «націнці», то в другому визначається зниження майбутньої вартості, "знижка" з її величини. (Diskont в перекладі з німецької означає «знижка».) Не дивно, що основною сферою застосування облікової ставки є дисконтування, процес, зворотний по відношенню до нарахування відсотків. Проте іноді облікова ставка використовується і для нарощення. У цьому випадку говорять про антисипативному відсотках.

За допомогою розглянутих вище ставок можуть нараховуватися як прості, так і складні відсотки. При нарахуванні простих відсотків нарощення початкової суми відбувається в арифметичній прогресії, а при нарахуванні складних відсотків - в геометричній. Спочатку більш детально розглянемо операції з простими відсотками.

Нарахування простих декурсівних і антисипативному відсотків проводиться у разі різним формулам:

декурсівних відсотки

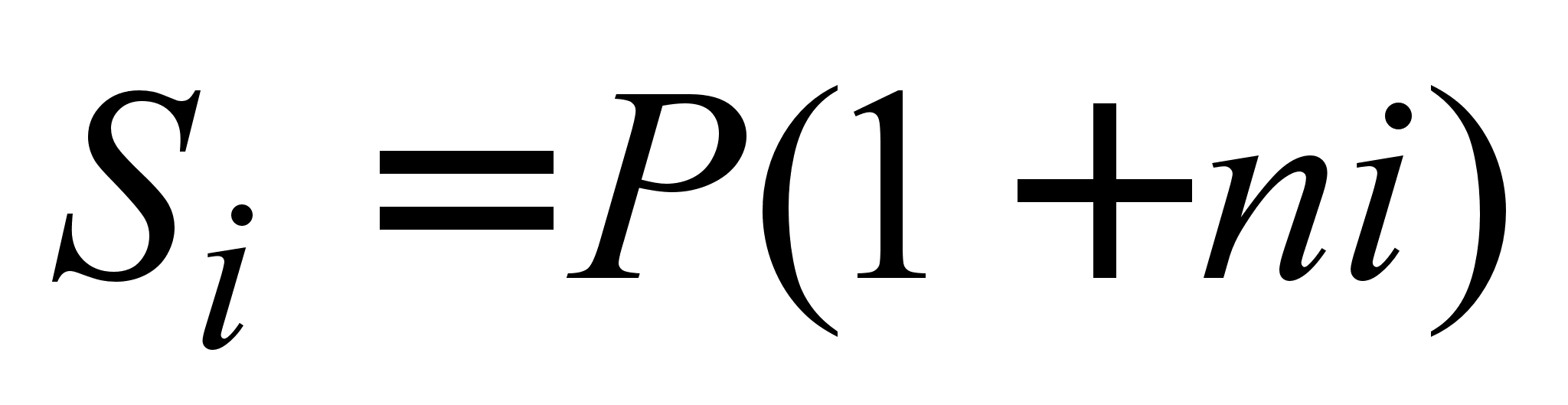; (2.1.3)

антисипативному відсотки

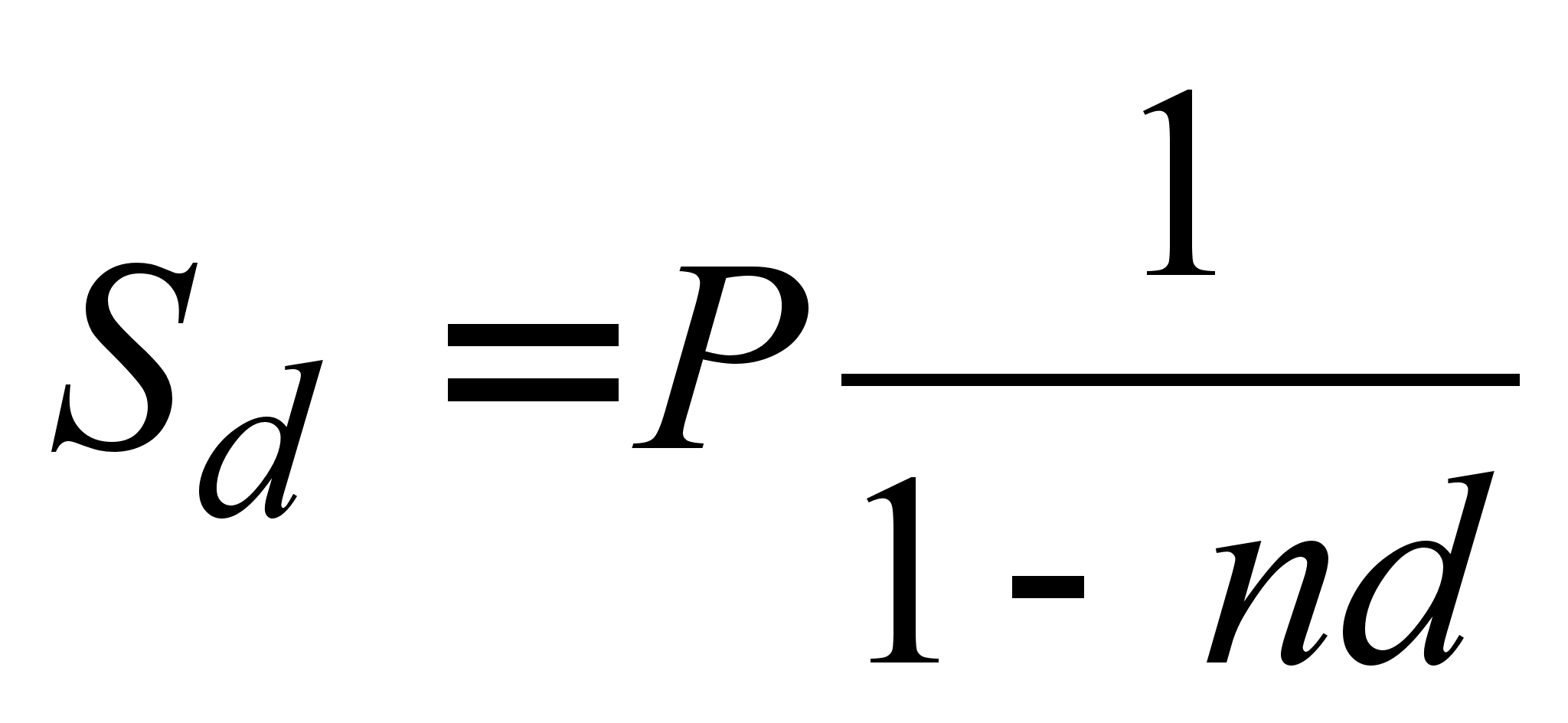, (2.1.4)

де n - тривалість позички, вимірювана в роках.

Для спрощення обчислень другі співмножники в формулах (2.1.3) і (2.1.4) називаються множниками нарощення простих відсотків: (1 + ni) - множник нарощення декурсівних відсотків; 1 / (1 - nd) - множник нарощення антисипативному відсотків.

Наприклад, позика в розмірі 1 млн. Руб. видається терміном на 0,5 року під 30% річних. У разі декурсівних відсотків нарощена сума (Si) дорівнюватиме 1,15 млн. Руб. (1 (1 + 0,5  0,3), а сума нарахованих відсотків (I) - 0,15 млн. Руб. (1,15 - 1). Якщо ж нараховувати відсотки по антисипативному методу, то нарощена величина (Sd ) складе 1,176 млн. руб. (1 (1 / (1 - 0,5  0,3), а сума відсотків (D) - 0,176 млн. руб. Нарощення по антисипативному методу завжди відбувається швидшими темпами, ніж при використанні процентної ставки. Тому банки використовують цей метод для нарахування відсотків по видаваних ними позичкам в періоди високої інфляції. Однак потрібно зазначити істотний недолік антисипативного методу: як видно з формули ( 2.1.4), при n = 1 / d, знаменник дробу звертається в нуль і вираз втрачає сенс.

Взагалі, нарахування відсотків з використанням ставки, призначеної для виконання прямо протилежної операції - дисконтування, - носить відтінок якоїсь «неприродності» і іноді породжує плутанину (аналогічну тій, яка може виникнути у роздрібного торговця, якщо він переплутає правила визначення знижок і націнок на свої товари ). З позиції математики ніякої складності тут немає, перетворивши (2.1.1), (2) і (4), отримуємо

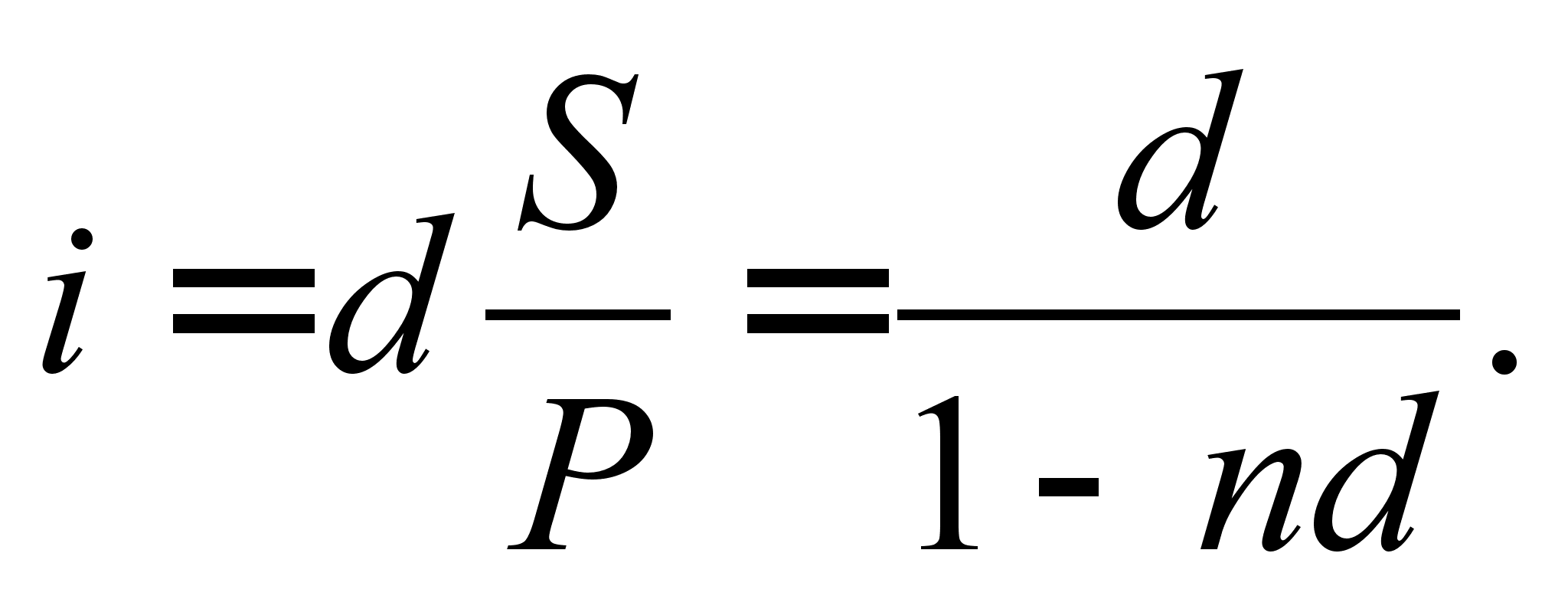(2.1.5)

Дотримуючись цю умову, можна отримувати еквівалентні результати, нараховуючи відсотки як за формулою (2.1.3), так і за формулою (2.1.4).

Антисипативному методом нарахування відсотків зазвичай користуються в чисто технічних цілях, зокрема для визначення суми, дисконтування якої по заданих облікової ставки і терміну дасть шуканий результат. У наступному параграфі будуть розглянуті подібні ситуації.

Як правило, процентні ставки встановлюються в річному обчисленні, тому вони називаються річними. Особливість простих відсотків в тому, що частота процесів нарощення протягом року не впливає на результат, т. Е. Немає ніякої різниці - нараховувати 30% річних один раз на рік або по 15% річних - два рази. Проста ставка 30% річних при одному нарахуванні на рік називається еквівалентній простий ставці 15% річних при нарахуванні один раз на півроку. Дана властивість пояснюється тим, що процес нарощення за простою відсоткової ставки є арифметичну прогресію з першим членом
a1 = P і різницею d = (P  i).

P, P + (P  i), P + 2 (P  i), P + 3 (P  i), ..., P + (k - 1) (P  i)

Нарощена сума S є не що інше, як останній k-й член цієї прогресії (S = ak = P + nPi), термін позики n дорівнює k - 1. Тому, якщо збільшити n і водночас пропорційно зменшити i, то величина кожного члена прогресії , в тому числі і останнього, залишиться незмінною.

Однак тривалість позички n (або іншої фінансової операції, пов'язаної з нарахуванням відсотків) необов'язково має дорівнювати року або цілому числу років. Навпаки, прості відсотки найчастіше використовуються при короткострокових (тривалістю менше року) операціях. В цьому випадку виникає проблема визначення тривалості позички і тривалості року в днях. Якщо позначити тривалість року в днях буквою K (цей показник називається тимчасової базою), а кількість днів користування позичкою - t, то використане в формулах (2.1.3) і (2.1.4) позначення кількості повних років n можна буде висловити як t / K. Підставивши цей вираз в (2.1.3) і (2.1.4), отримаємо:

для декурсівних відсотків

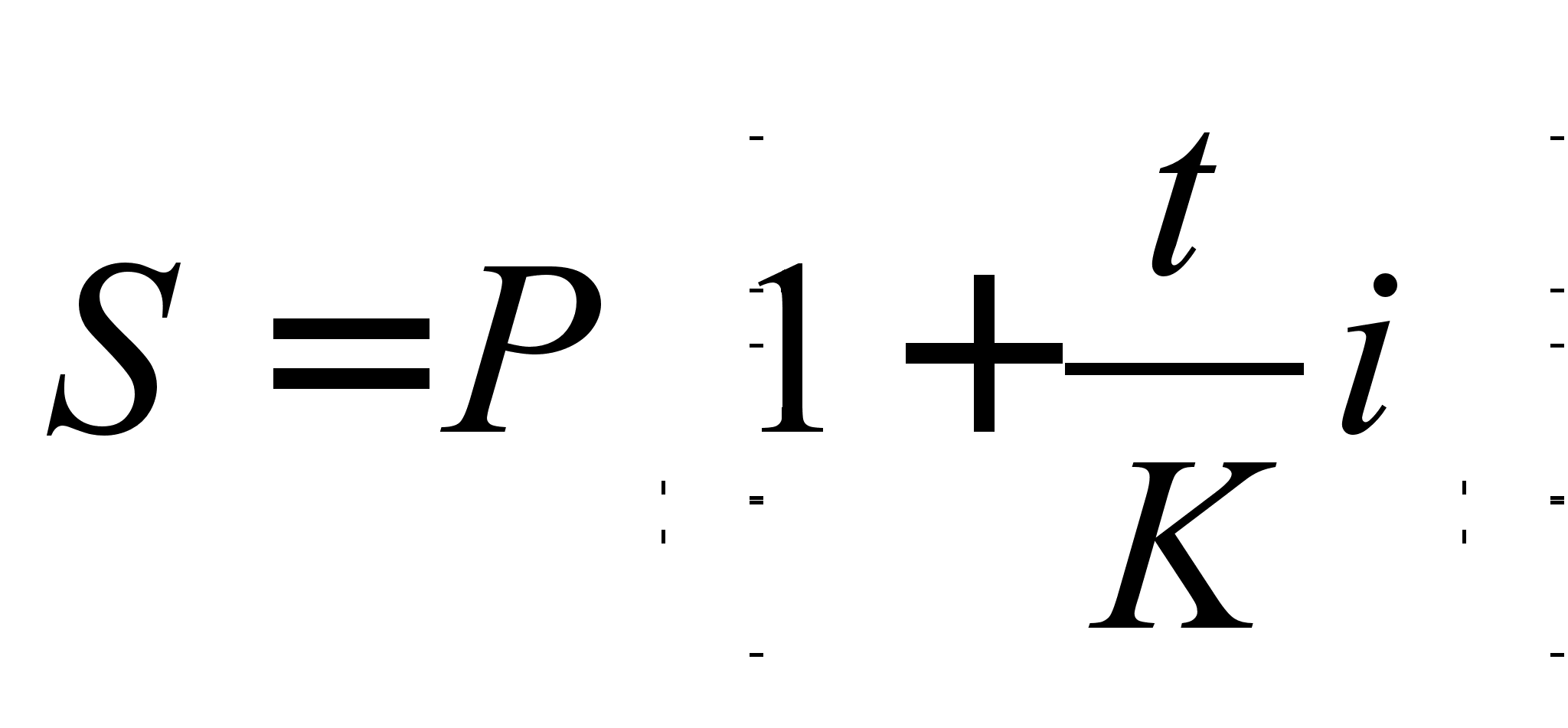; (2.1.6)

для антисипативному відсотків

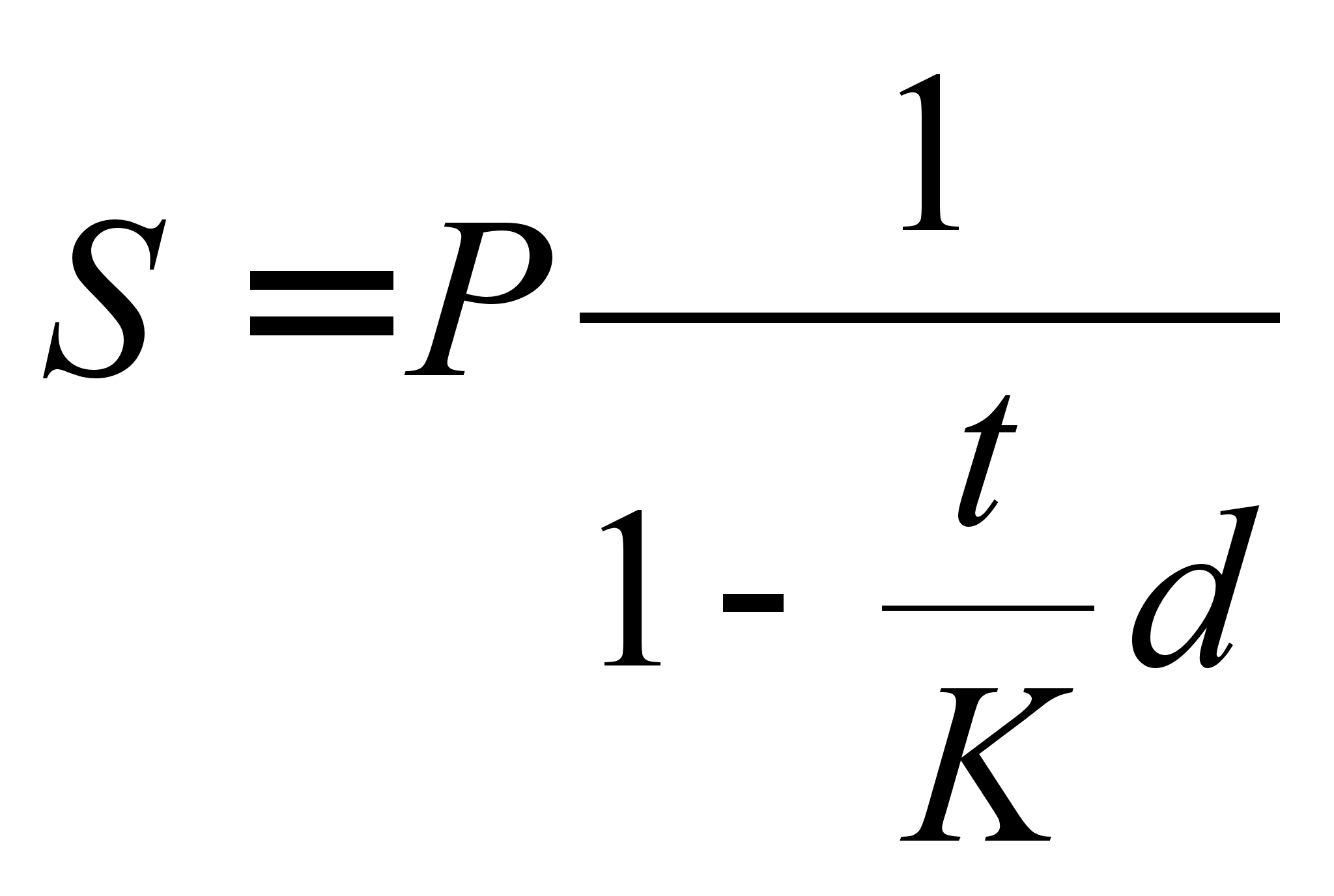. (2.1.7)

У різних випадках можуть застосовуватися свої способи підрахунку числа днів в році (угоду з підрахунку днів). Рік може прийматися рівним 365 або 360 дням (12 повних місяців по 30 днів у кожному). Складність представляють підрахунки у високосний рік. Наприклад, позначення ACT / 360 (actual over 360) вказує на те, що тривалість року приймається рівною
360 дням. Однак виникає питання, а як при цьому визначається тривалість позички? Наприклад, якщо кредит видається 10 березня з терміном повернення 17 червня цього ж року, як вважати його тривалість - за календарем або виходячи з припущення, що будь-який місяць дорівнює 30 дням? Безумовно, в кожному конкретному випадку може бути обраний свій оригінальний спосіб підрахунку числа днів, проте на практиці вироблені деякі загальні принципи, знання яких може допомогти зорієнтуватися в будь-якій конкретній ситуації.

Якщо тимчасова база (K) приймається рівної 365 (366) дням, то відсотки називаються точними. Якщо тимчасова база дорівнює 360 дням, то говорять про комерційних, або звичайних, відсотках. У свою чергу підрахунок тривалості позички може бути або наближеним, коли виходять з тривалості року в 360 днів, або точним - за календарем або за спеціальною таблицею номерів днів на рік. Визначаючи наближену тривалість позички, спочатку підраховують число повних місяців і множать його на 30. Потім додають число днів в неповних місяцях. Загальним для всіх способів підрахунку є правило: день видачі і день повернення кредиту вважаються за 1 день (назвемо його граничний день). У наведеному вище умовному прикладі точна тривалість позички складе за календарем 99 днів (21 день в березні + 30 днів в квітні + 31 день в травні + 16 днів в червні + 1 граничний день). Той же результат буде отримано, якщо використовувати таблицю номерів днів на рік (10 березня має порядковий номер 69, а 17 червня - 168). Якщо ж використовувати наближений спосіб підрахунку, то тривалість позички складе 98 днів (21 + 2  30 + 16 + 1).

Найбільш часто зустрічаються такі комбінації тимчасової бази й тривалості позички (цифри в дужках позначають відповідно величину t і K):

1) точні відсотки з точним числом днів (365/365);

2) звичайні (комерційні) відсотки з точною тривалістю позички (365/360);

3) звичайні (комерційні) відсотки з наближеною тривалістю позички (360/360).

Відмінності в способах підрахунку днів можуть здатися несуттєвими, однак при великих сумах операцій та високих відсоткових ставках вони досягають дуже пристойних розмірів. Припустимо, що позика в розмірі 10 млн. Руб. видана 1 травня з поверненням 31 грудня цього року під 45% річних (проста процентна ставка). Визначимо нарощену суму цього кредиту по кожному з трьох способів. Табличне значення точної тривалості позички одно 244 дням (365 - 121); наближена тривалість - 241 дня (6  30 + 30 + 30 + 1).

1) 10  (1 + 0,45  244/365) = 13,008 млн. Руб .;

2) 10  (1 + 0,45  244/360) = 13,05 млн. Руб .;

3) 10  (1 + 0,45  241/360) = 13,013 млн. Руб.

Різниця між найбільшою і найменшою величинами
(13,05 - 13,008) означає, що боржник буде змушений заплатити додатково 42 тис. Рублів тільки за те, що погодився (або не звернув уваги) на застосування другого способу нарахування відсотків.

Зворотною завданням по відношенню до нарахування відсотків є розрахунок сучасної вартості майбутніх грошових надходжень (платежів), або дисконтування. В ході дисконтування за відомою майбутньої вартості S і заданим значенням відсоткової (облікової) ставки і тривалості операції перебуває початкова (сучасна, наведена чи поточна) вартість P. Залежно від того, яка саме ставка - проста відсоткова чи проста облікова - застосовується для дисконтування, розрізняють два види: математичне дисконтування і банківський облік.

Метод банківського обліку отримав свою назву від однойменної фінансової операції, в ході якої комерційний банк викуповує у власника (враховує) простий або переказний вексель за ціною нижче номіналу до закінчення зазначеного на цьому документі терміну його погашення. Різниця між номіналом і викупної ціною утворює прибуток банку від цієї операції і називається дисконт (D). Для визначення розміру викупної ціни (а отже, і суми дисконту) застосовується дисконтування за методом банківського обліку. При цьому використовується проста облікова ставка d. Викупна ціна (сучасна вартість) векселі визначається за формулою

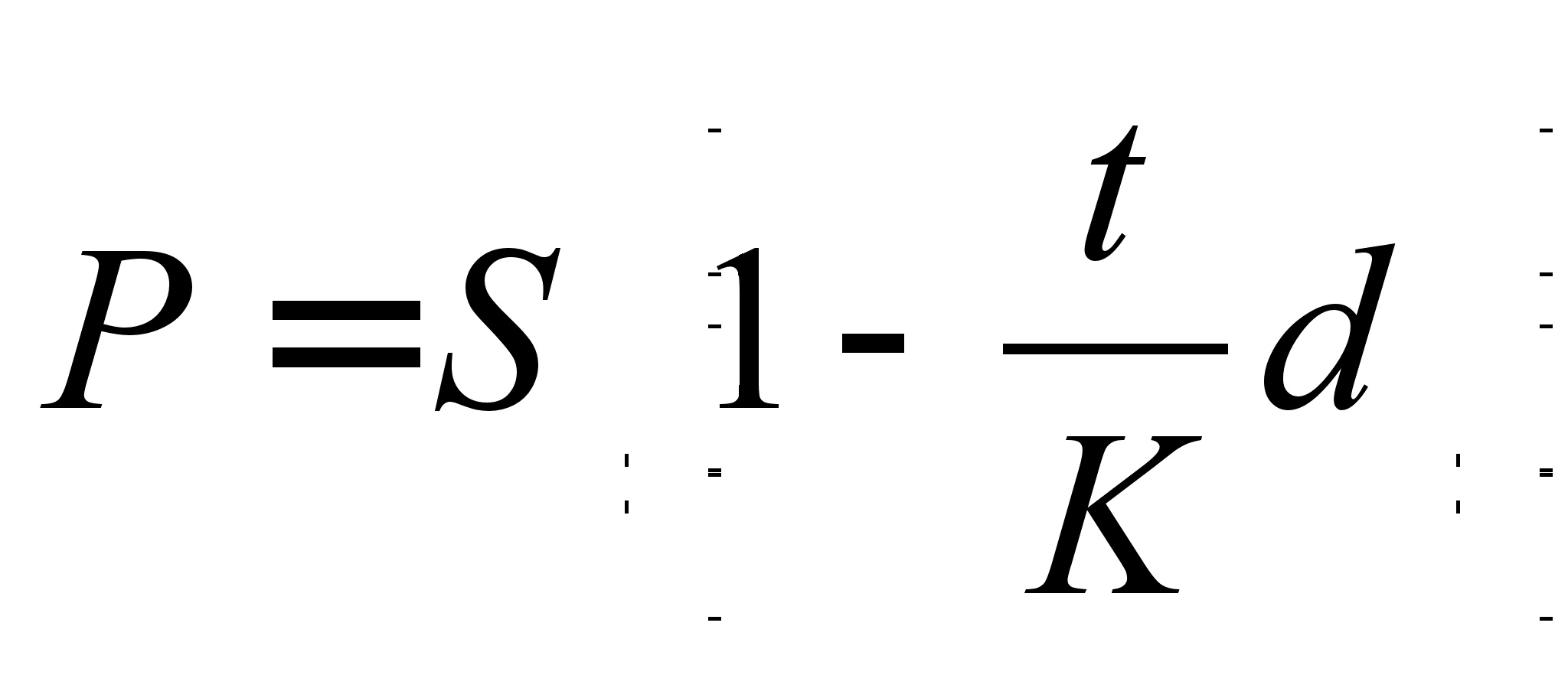, (2.1.8)

де t - термін, що залишається до погашення векселя, в днях. Другий співмножник цього виразу (1 - (t / k)  d) називається дисконтним множником банківського обліку за простими відсоткам. Як правило, при банківському обліку застосовуються звичайні відсотки з точною тривалістю позички (другий варіант). Наприклад, власник векселя номіналом 25 тис. Руб. звернувся в банк з пропозицією врахувати його за 60 днів до настання терміну погашення. Банк згоден виконати цю операцію за простою обліковою ставкою 35% річних: викупна ціна векселя

P = 25000 (1 - 60/360  0,35) = 23541,7 грн .;

сума дисконту

D = S - P = 25000 - 23541,7 = 1458,3 руб.

При математичному дисконтуванні використовується проста процентна ставка i. Розрахунки виконуються за формулою

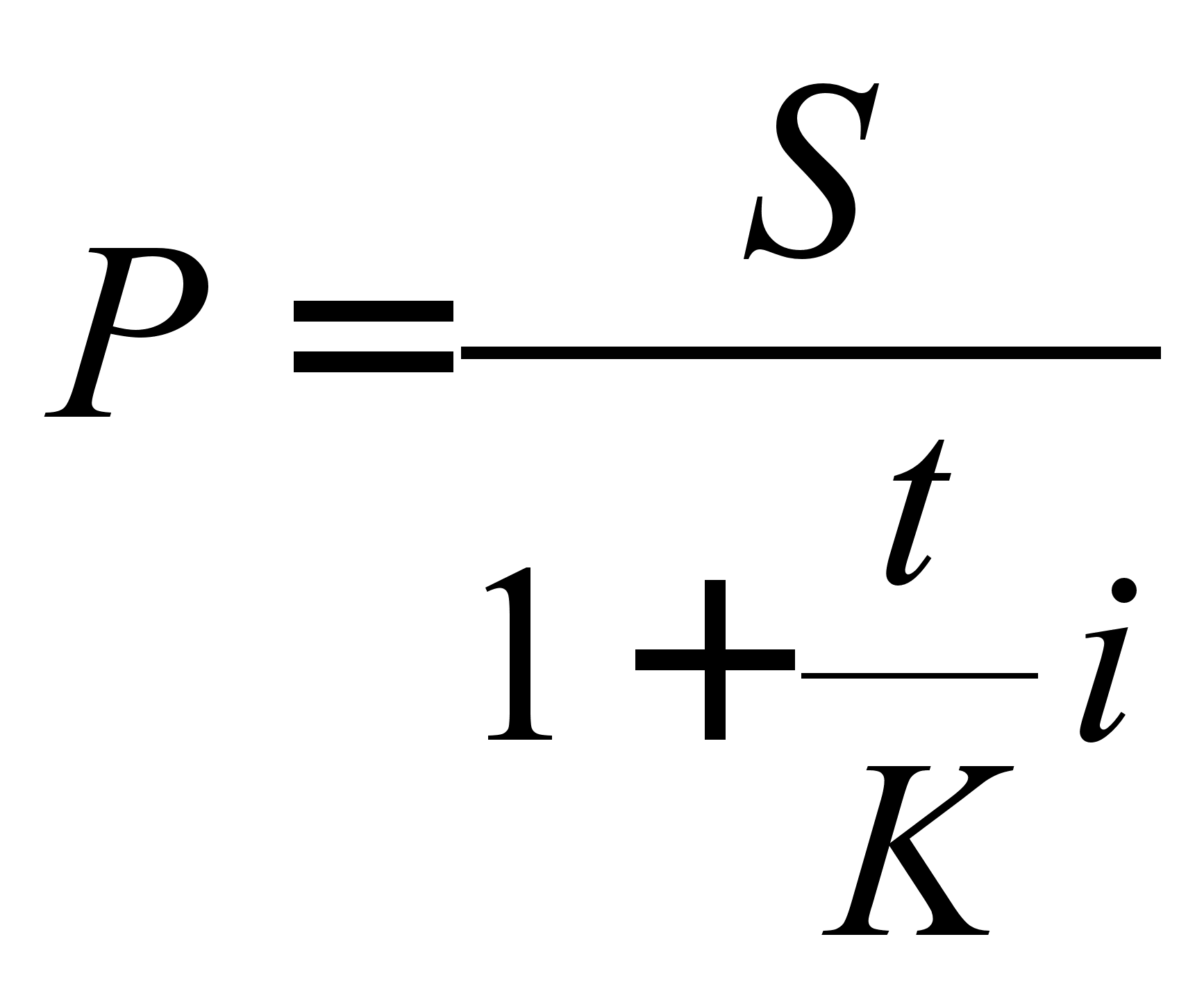. (2.1.9)

Вираз 1 / (1 + (t / k) i) називається дисконтним множником математичного дисконтування за простими відсоткам.

Цей метод застосовується у всіх інших (крім банківського обліку) випадках, коли виникає необхідність визначити сучасну величину суми грошей, яка буде отримана в майбутньому. Наприклад, покупець зобов'язується оплатити постачальнику вартість закуплених товарів через 90 днів після поставки в сумі 1 млн. Руб. Рівень простий відсоткової ставки становить 30% річних (звичайні відсотки). Отже, поточна вартість товарів дорівнюватиме

P = 1 / (1 + 90/360  0,3) = 0,93 млн. Руб.

Застосувавши до цих умов метод банківського обліку, одержимо

P = 1 (1 - 90/360  0,3) = 0,925 млн. Руб.

Другий варіант виявляється більш вигідним для кредитора. Слід пам'ятати, що якихось жорстких вимог вибору того або іншого методу виконання фінансових розрахунків не існує. Ніхто не може заборонити учасникам фінансової операції вибрати в даній ситуації метод математичного дисконтування чи банківського обліку. Існує, мабуть, єдина закономірність - банками, як правило, вибирається метод, вигідніший для кредитора (інвестора).

Основна область! Застосування простих відсоткової и облікової ставок - короткострокові фінансові операции, длительность якіх ставити менше 1 року. Обчислення з простими ставками не враховують можливості реінвестування нарахованих відсотків, тому що нарощування і дисконтування виробляються щодо незмінною вихідної суми P чи S. На відміну від них складні ставки відсотків враховують можливість реінвестування відсотків, так як в цьому випадку нарощення виробляється за формулі не арифметичної, а геометричній прогресії, першим членом якої є початкова сума P, а знаменник дорівнює (1 + i)

P, P (1 + i), P (1 + i) 2, P (1 + i) 3, ..., P (1 + i) n,

де число років позички n менше числа членів прогресії k на 1 (n = k - 1).

Нарощена вартість (останній член прогресії) перебувають розслідування щодо формулі

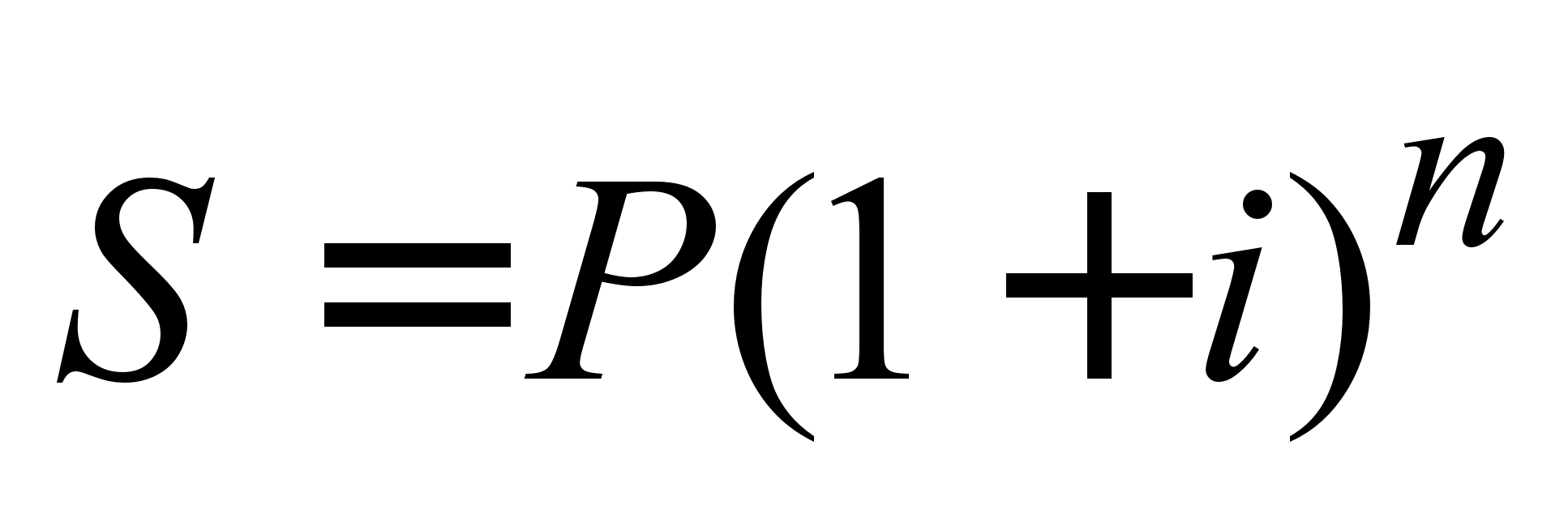, (2.1.10),

де (1 + i) n - множник нарощення декурсівних складних відсотків.

З позицій фінансового менеджменту використання складних відсотків більш переважно, так як визнання можливості власника в будь-який момент інвестувати свої кошти з метою отримання доходу - наріжний камінь всієї фінансової теорії. При використанні простих відсотків ця можливість часто не враховується, тому результати обчислень виходять менш коректними. Проте при короткострокових фінансових операціях як і раніше широко застосовуються обчислення простих відсотків. Деякі математики вважають це прикрим пережитком, які залишилися з тих пір, коли у фінансистів не було під рукою калькуляторів і вони були змушені вдаватися до більш простим, хоча і менш точним способам розрахунку. Представляється можливим і дещо інше пояснення даного факту. При тривалості операцій менш одного року (n <1) нарахування простих відсотків забезпечує отримання результатів навіть вигідніших для кредитора, ніж використання складних відсотків. Вище вже відзначалася закономірність вибору банками саме таких, вигідніших для кредитора способів. Тому було б наївно недооцінювати обчислювальні потужності сучасних банків та інтелектуальний потенціал їхніх співробітників, вважаючи, що вони використовують грубі методи розрахунків тільки через їх низьку трудомісткості. Важко уявити собі банкіра, хоча б на секунду забуває про власну вигоду.

Сама по собі складна процентна ставка i нічим не відрізняється від простої і розраховується за такою ж формулою (2.1.1). Складна облікова ставка визначається за формулою (2.1.2). Так само як і у випадку простих відсотків, можливе застосування складної облікової ставки для нарахування відсотків (антисипативному метод)

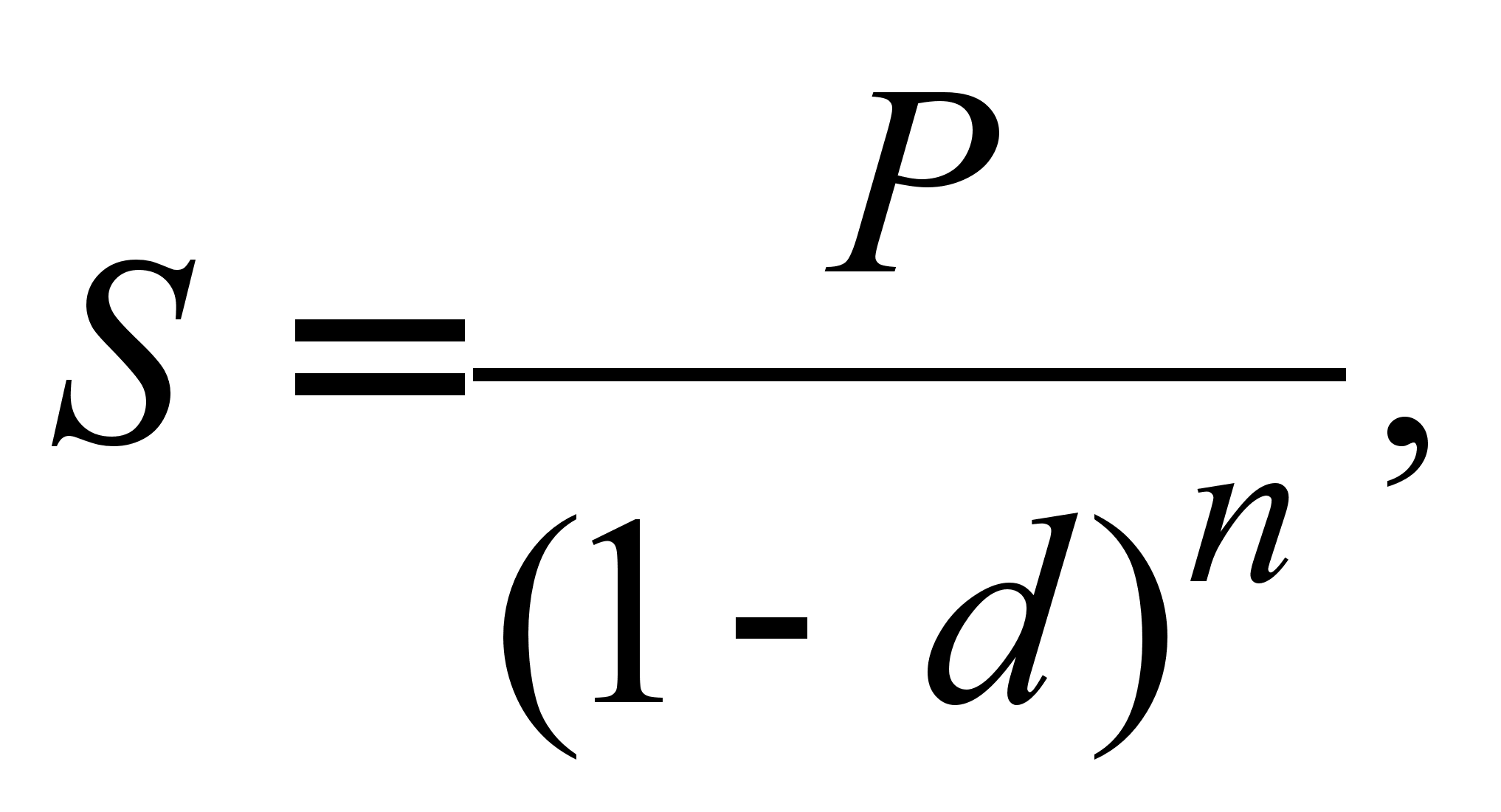(2.1.11)

де множник перед Р - множник нарощення складних антисипативному відсотків.

Однак практичне застосування такого способу нарощення відсотків досить обмежене, швидше за це з розряду фінансової екзотики.

Як вже зазначалося, найбільш широко складні відсотки застосовуються при аналізі довгострокових фінансових операцій (n> 1). На великому проміжку часу в повній мірі проявляється ефект реінвестування, нарахування «відсотків на відсотки». У зв'язку з цим питання вимірювання тривалості операції і тривалості року в днях в разі складних відсотків стоїть менш гостро. Як правило, неповне кількість років висловлюють дробовим числом через кількість місяців (3/12 чи 7/12), не вдаючись у точніші підрахунки днів. Тому у формулі нарахування складних відсотків число років практично завжди позначається буквою n, а не виразом t / K, як це прийнято для простих відсотків. Найбільш педантичні кредитори, приймаючи до уваги велику ефективність простих відсотків на коротких відрізках часу, використовують змішаний порядок нарахування відсотків у разі, коли термін операції (позик), не дорівнює цілому числу років: складні відсотки нараховуються на період, який вимірюється цілими роками, а відсотки за дробову частина терміну - за простою відсоткової ставки

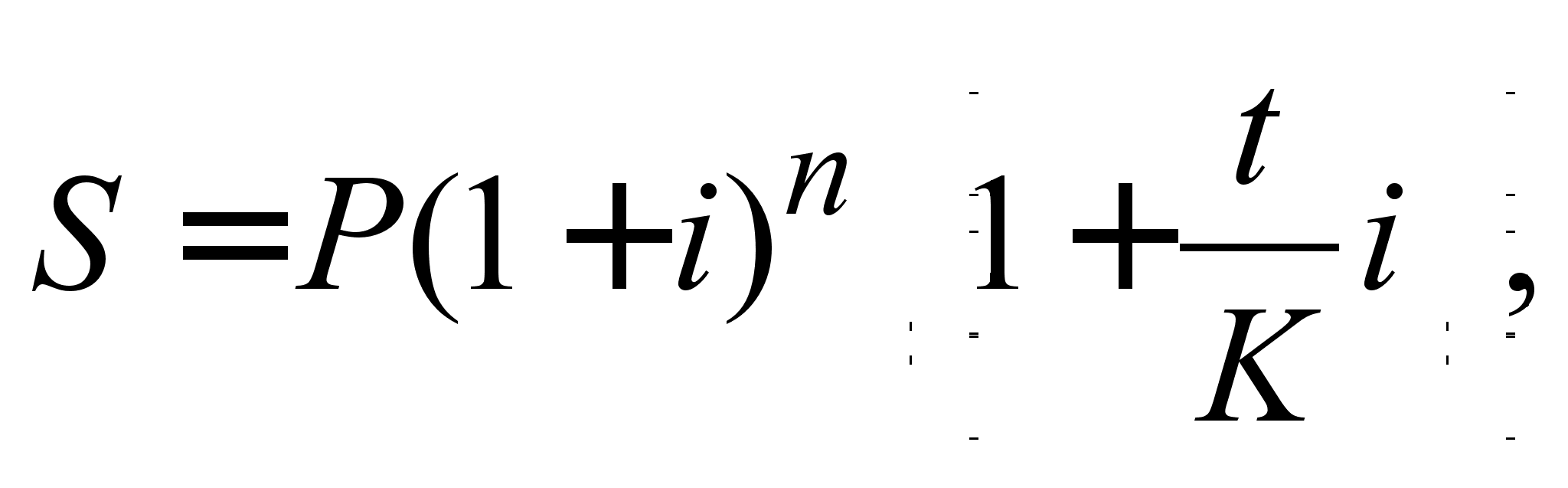(2.1.12)

де a - число повних років у складі тривалості операції; t - число днів в відрізку часу, що припадає на неповний рік; K тимчасова база.

В цьому випадку знову виникає необхідність виконання календарних обчислень по розглянутим вище правилам. Наприклад, позика в 3 млн. Руб. видається 1 січня 1997 року по 30 вересня 1999 р під 28% річних (процентна ставка). У разі нарахування складних відсотків за весь термін користування грошима нарощена сума складе

S = 3 (1 + 0,28) ^ (2 + 9/12) = 5,915 млн. Руб.

Якщо ж використовувати змішаний спосіб (наприклад, комерційні відсотки з точним числом днів), то отримаємо

S = 3 (1 + 0,28) ^ 2 (1 + 272/360  0,28) = 6 млн. Руб.

Таким чином, педантичність кредитора в даному випадку виявилася зовсім не зайвою і була винагороджена додатковим доходом в сумі 85 тис. Руб.

Важлива особливість складних відсотків - залежність кінцевого результату від кількості нарахувань протягом року. Тут знову позначається вплив реінвестування нарахованих відсотків: база нарахування зростає з кожним новим нарахуванням, а не залишається незмінною, як у випадку простих відсотків. Наприклад, якщо нараховувати 20% річних 1 раз в рік, то початкова сума в 1 тис. Руб. зросте до кінця року до 1,2 тис. руб. (1 (1 + 0,2)). Якщо ж нараховувати по 10% кожні півроку, то майбутня вартість складе 1,21 тис. Руб. (1 (1 + 0,1) (1 + 0,1)), при поквартальном нарахуванні по 5% вона зросте до 1,216 тис. Руб. У міру збільшення числа нарахувань (m) і тривалості операції ця різниця буде дуже сильно збільшуватися. Якщо розділити суму нарахованих відсотків при щоквартальному нарощенні на початкову суму, то вийде 21,6% (0,216 / 1  100), а не 20%. Отже, складна ставка 20% при одноразовому і 20% (чотири рази по 5%) при поквартальном нарощенні призводять до різних результатів, т. Е. Не є еквівалентними. Цифра 20% відбиває вже не дійсну (ефективну), а номінальну ставку. Ефективною процентною ставкою вважається значення 21,6%. У фінансових розрахунках номінальну складну відсоткову ставку прийнято позначати буквою j. Формула нарощення по складним відсоткам при нарахуванні їх m разів на рік має вигляд

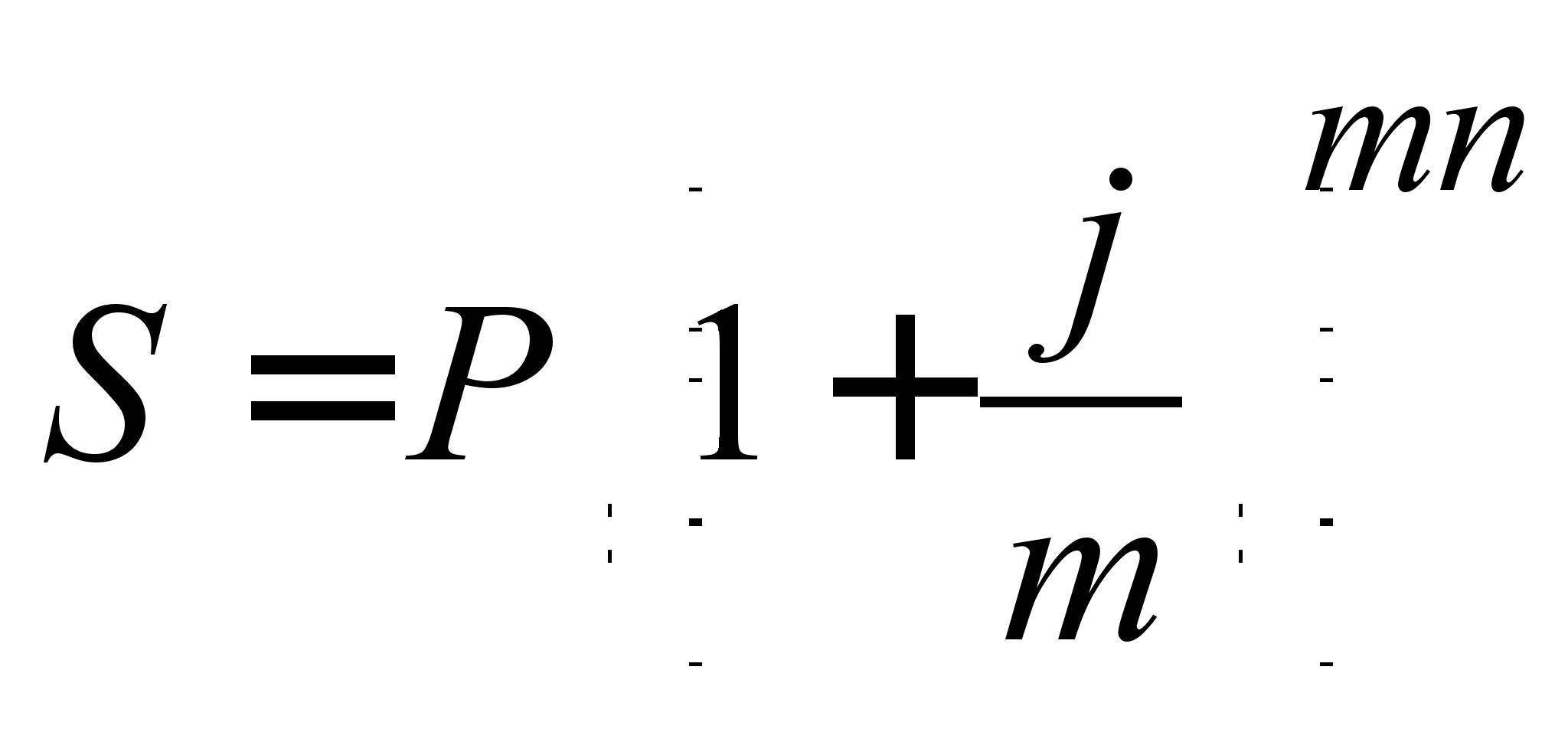, (2.1.13)

Наприклад, позика в сумі 5 млн. Руб. видана на 2 роки за номінальною складної відсоткової ставки 35% річних з нарахуванням відсотків два рази на рік. Майбутня сума до кінця терміну позики складе

S = 5 (1 + 0,35 / 2) ^ (2  2) = 9,531 млн. Руб.

При одноразовому нарахуванні її величина становила б лише 9,113 млн. Руб. (5 (1 + 0,35) ^ 2; зате при щомісячному нарахуванні повертати довелося б уже 9,968 млн. Руб. (5  1 + (0,35 / 12) ^
^ (12  2)).

При нарахуванні антисипативному складних відсотків, номінальна облікова ставка позначається буквою f, а формула нарощення набуває вигляду

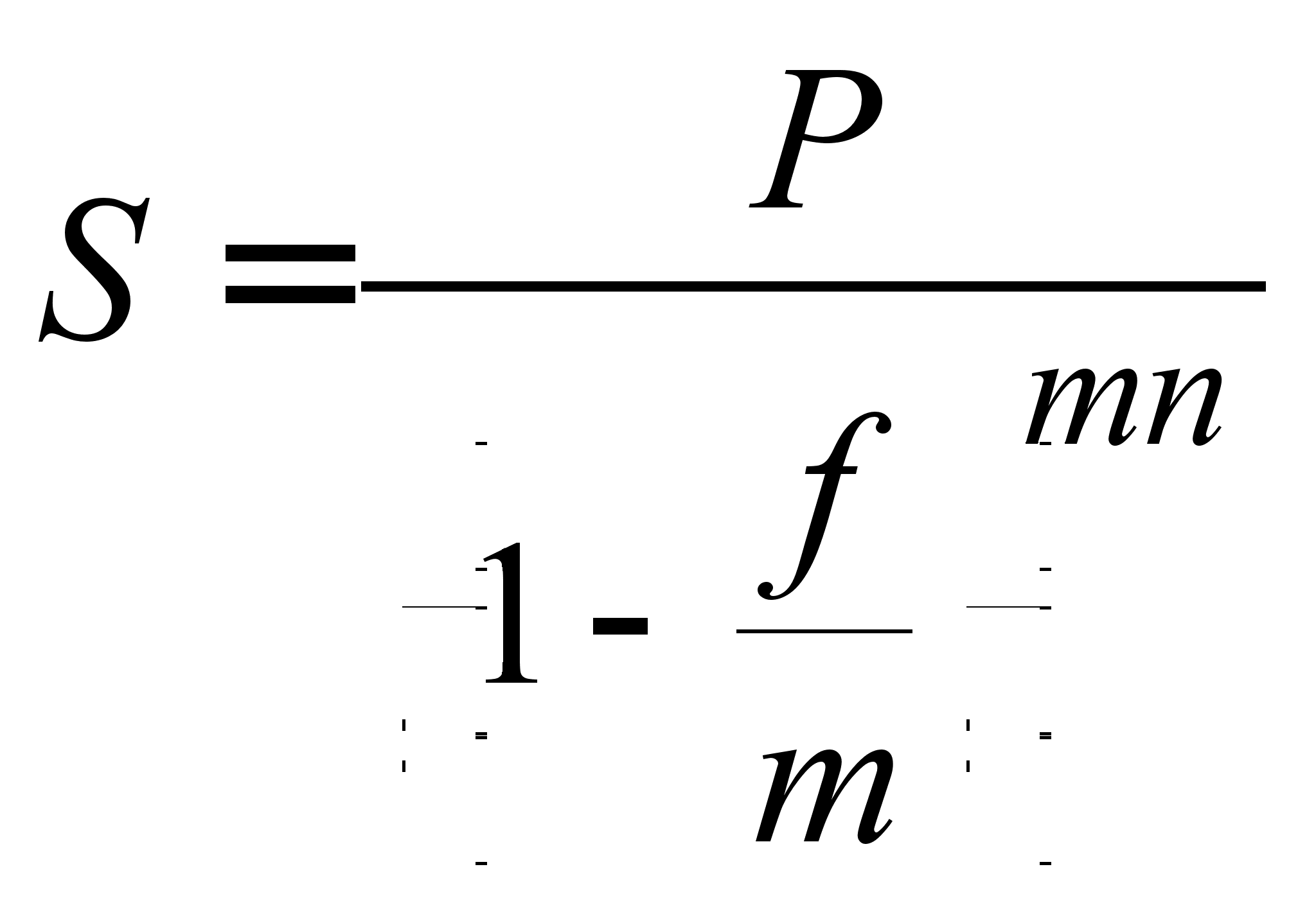. (2.1.14)

Вираз 1 / 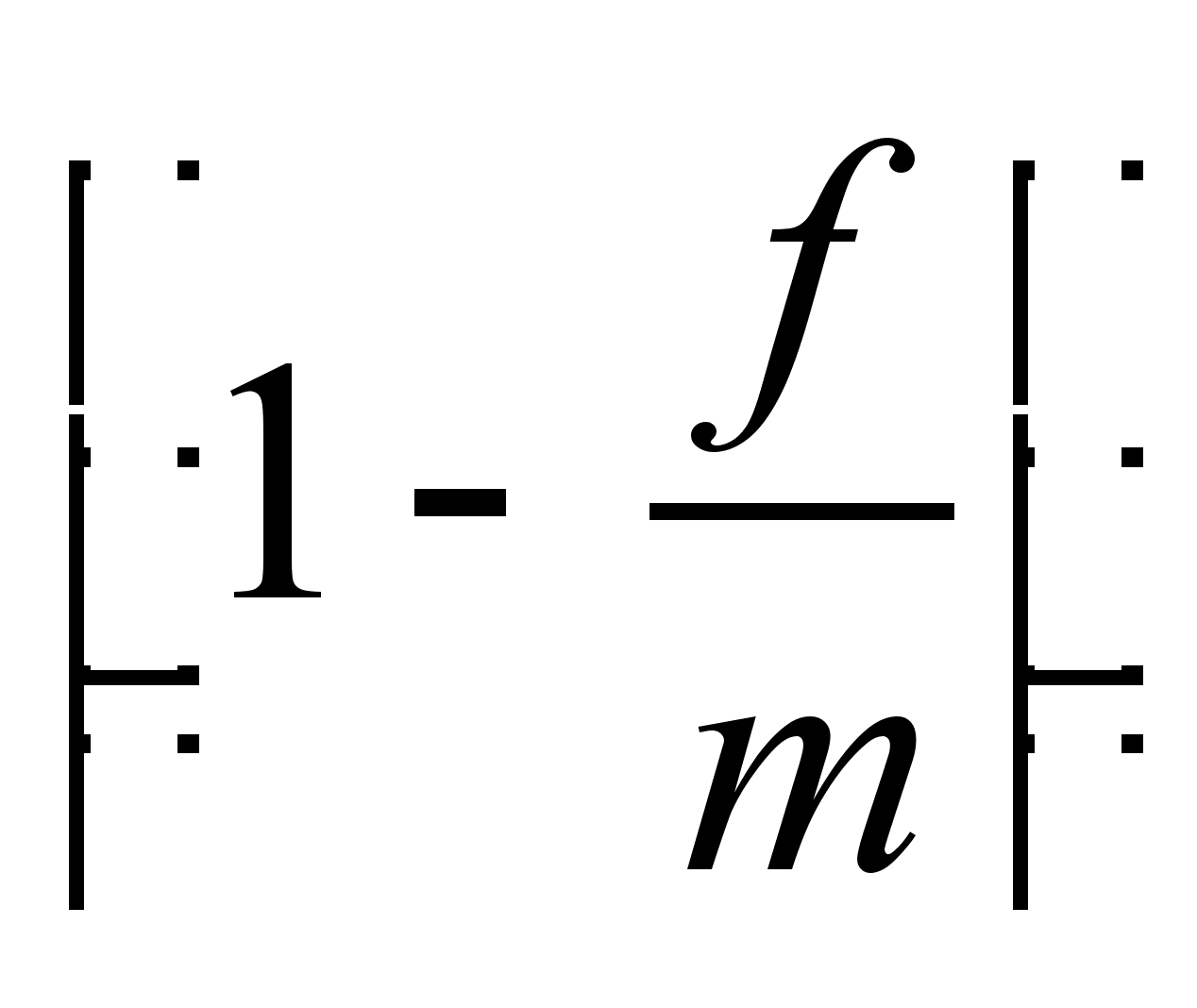^ Mn - множник нарощення за номінальною облікової ставки.

Дисконтування по складним відсоткам також може виконуватися двома способами - математичне дисконтування і банківський облік. Останній менш вигідний для кредитора, ніж облік за простою обліковою ставкою, тому використовується вкрай рідко. У разі одноразового нарахування відсотків його формула має вигляд

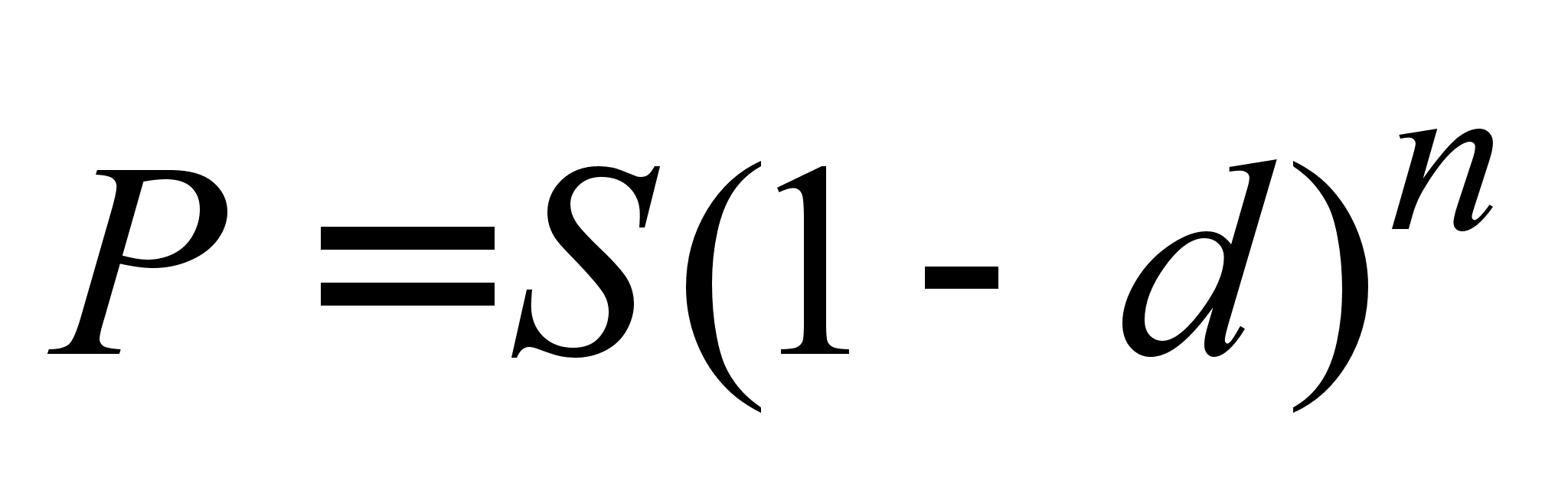, (2.1.15)

де (1 - d) n- дисконтний множник банківського обліку по складної облікової ставки.

При m> 1 отримуємо

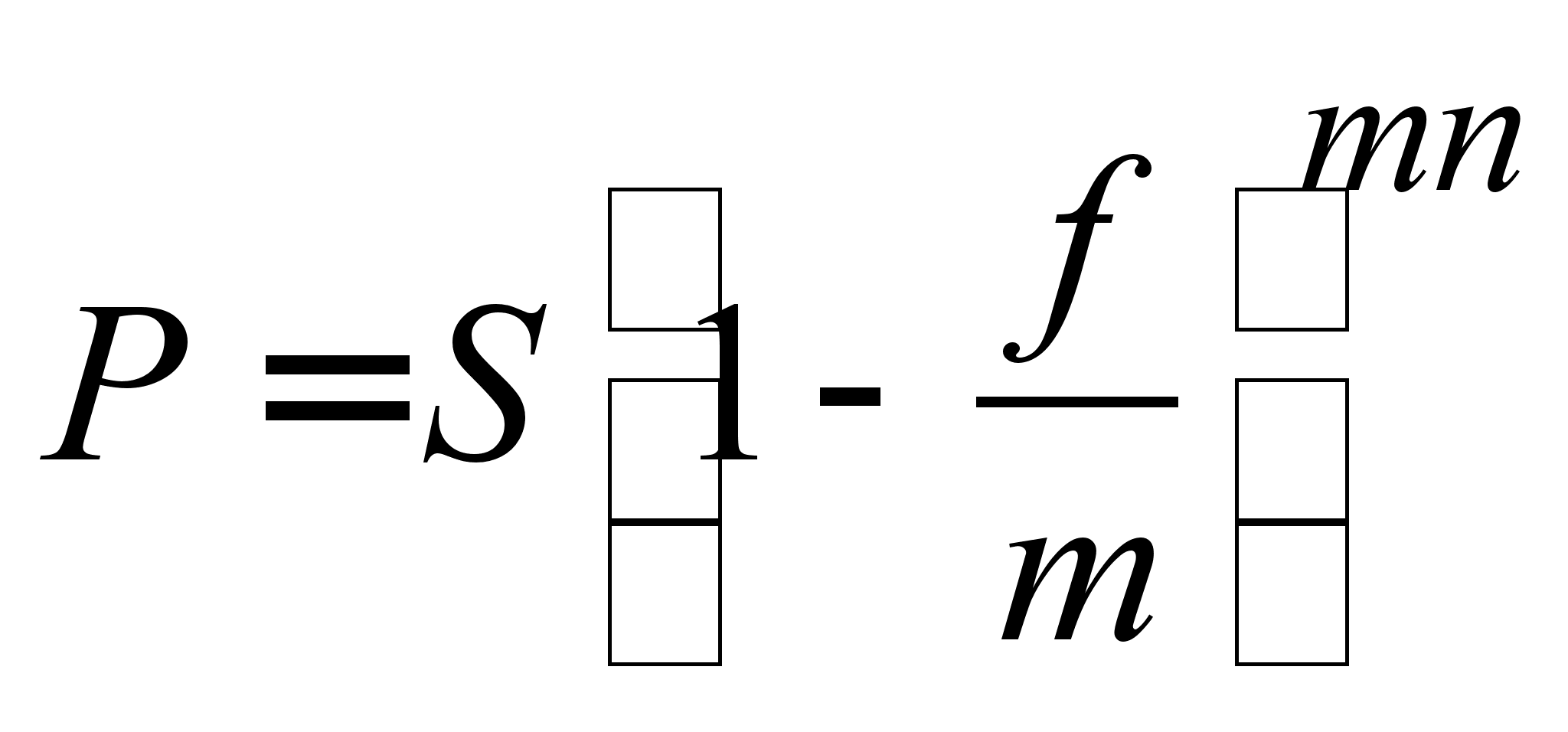, (2.1.16)

де f - номінальна складна облікова ставка; 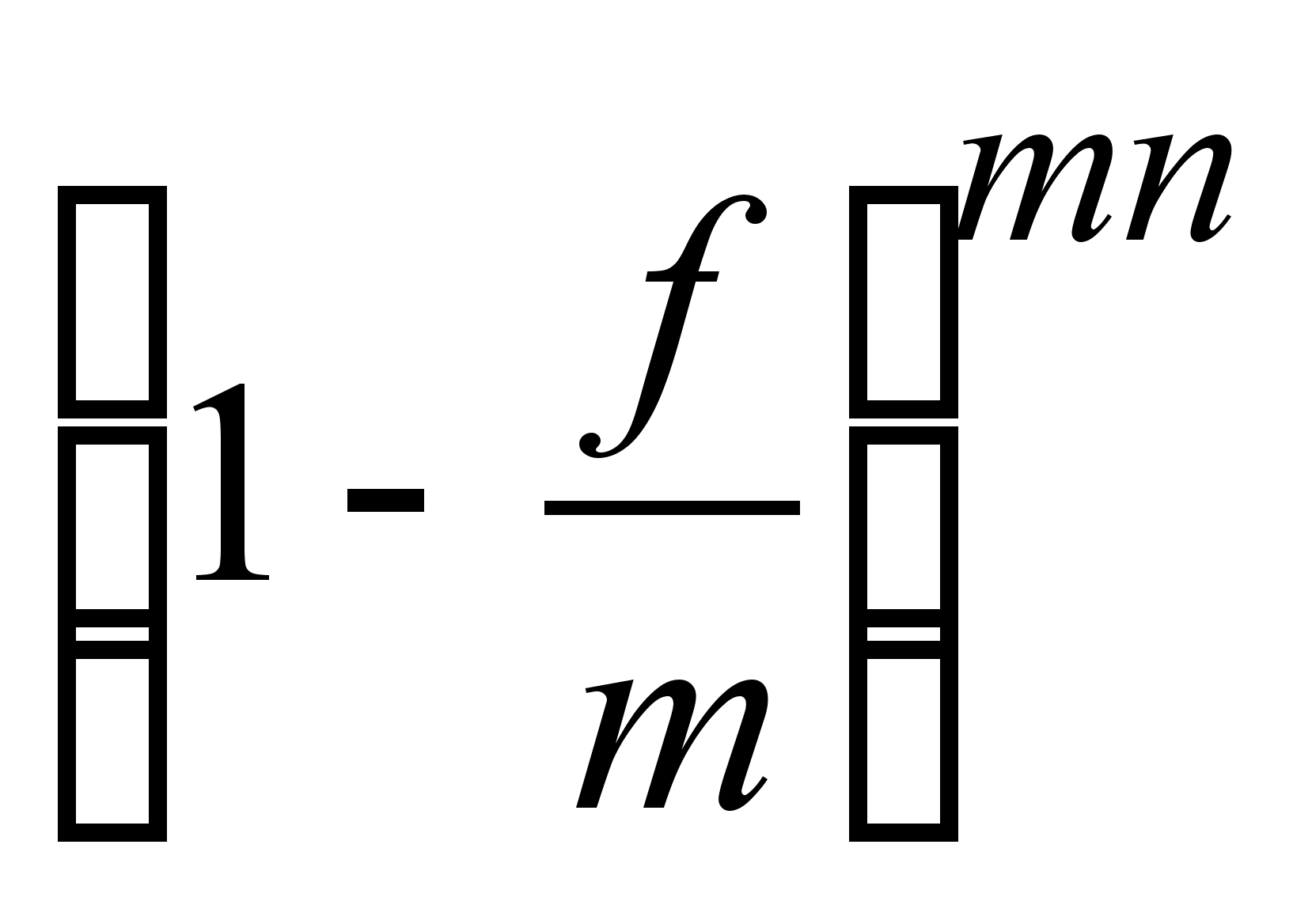- дисконтний множник банківського обліку по складної номінальною облікової ставки.

Більш широко поширене математичне дисконтування по складній процентній ставці i. Для m = 1 отримуємо

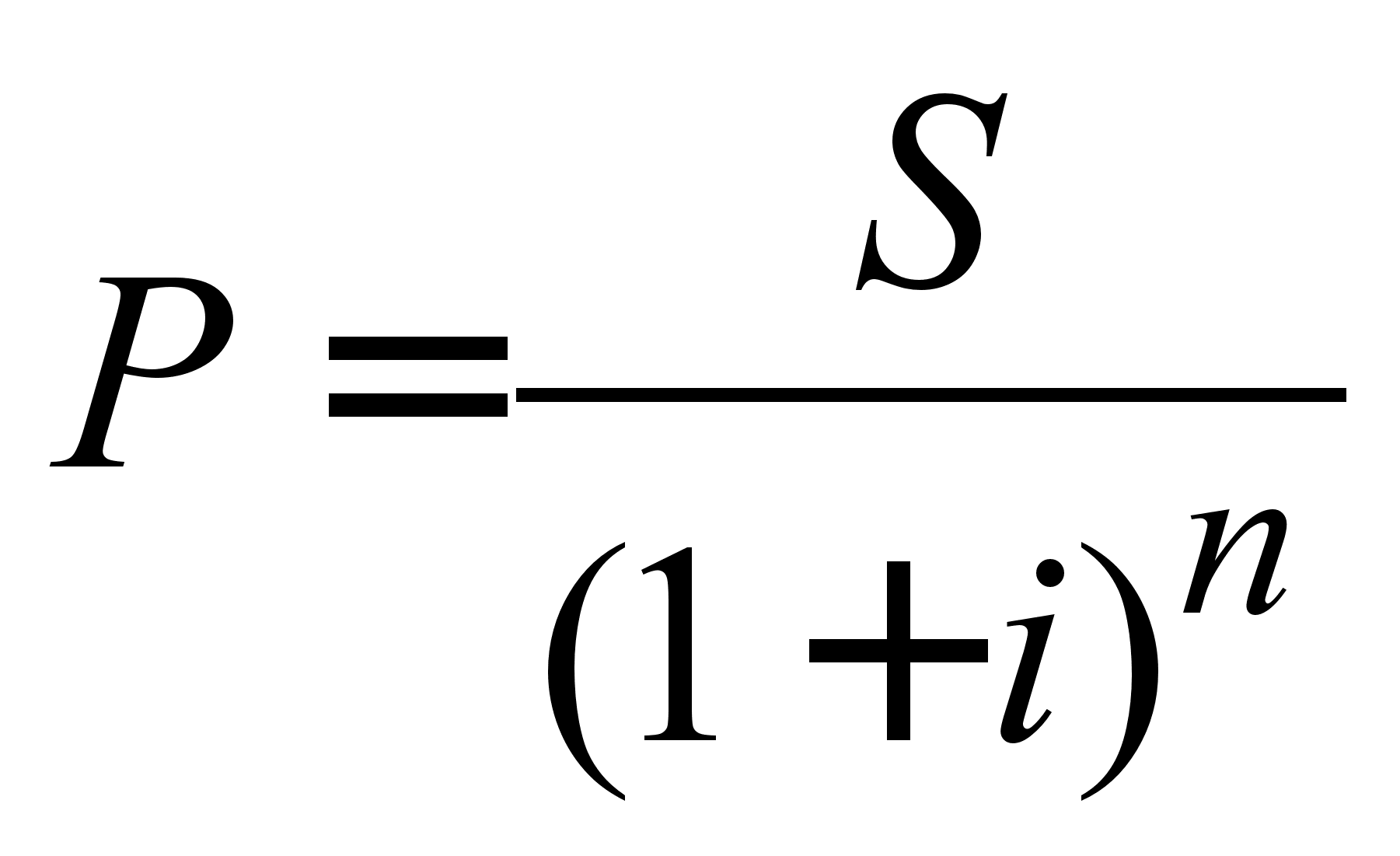, (2.1.17)

де 1 / (1 + i) n - дисконтний множник математичного дисконтування по складній процентній ставці.

При неодноразовому нарахуванні відсотків протягом року формула математичного дисконтування приймає вид

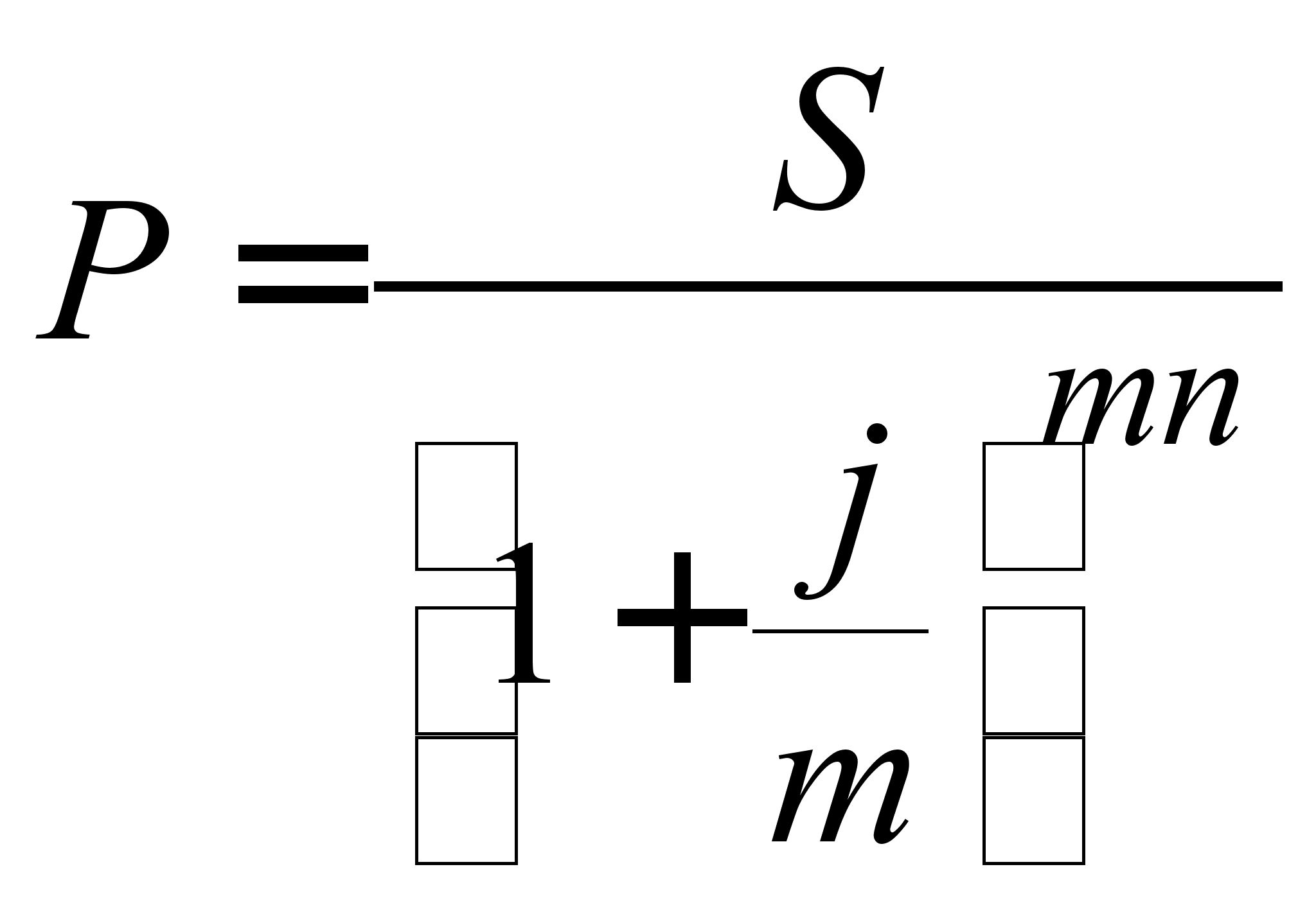, (2.1.18)

де j - номінальна складна процентна ставка; 1 / 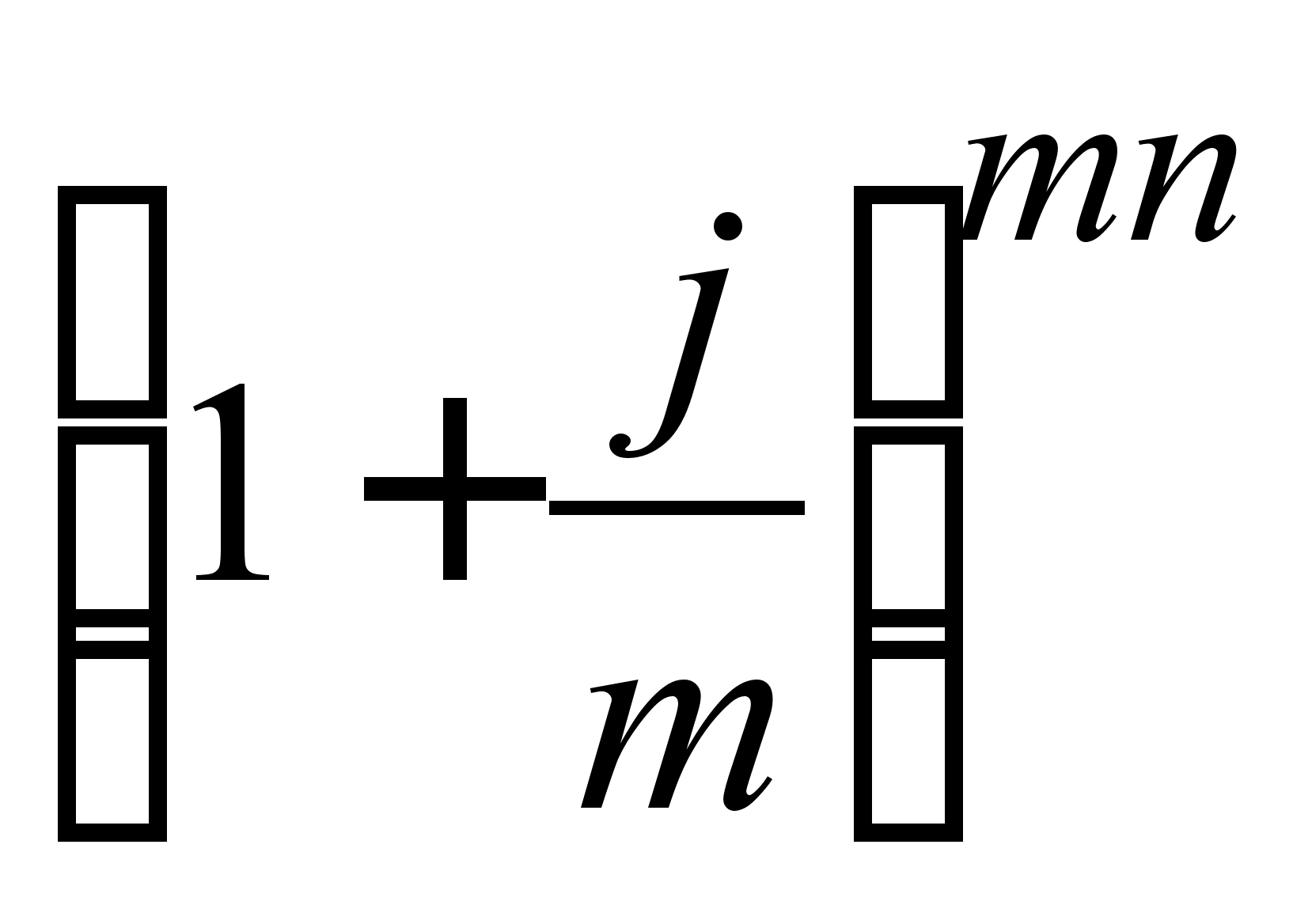- дисконтний множник математичного дисконтування по складній номінальній процентній ставці.

Наприклад, потрібно визначити сучасну вартість платежу в розмірі 3 млн. Руб., Який повинен надійти через 1,5 року. Відсоткова ставка становить 40%:

при m = 1 P = 3 / (1 + 0,4) ^ 1,5 = 1,811 млн. руб .;

при m = 2 (нарахування 1 раз в півріччя) P = (3 / (1 + 0,4 / 2) ^
^ (2  1,5) = 1,736 млн. Руб .;

при m = 12 (щомісячне нарахування) P = (3 / (1 + 0,4 / 12) ^
^ (12  1,5) = 1,663 млн. Руб.

У міру збільшення числа нарахувань відсотків протягом року (m) проміжок часу між двома суміжними нарахуваннями зменшується - при m = 1 цей проміжок дорівнює одному року, а при m = 12 - тільки 1 місяця. Теоретично можна уявити ситуацію, коли нарахування складних відсотків виробляється настільки часто, що загальне його число на рік прагне до нескінченності, тоді величина проміжку між окремими нарахуваннями наближатиметься до нуля, т. Е. Нарахування стане практично безперервним. Така, на перший погляд гіпотетична ситуація має важливе значення для фінансів, тому при побудові складних аналітичних моделей (наприклад, при розробці масштабних інвестиційних проектів) часто застосовують безперервні відсотки. Безперервна процентна ставка (очевидно, що при безперервному нарахуванні мова може йти тільки про складні відсотках) позначається буквою δ (читається «дельта»), часто цей показник називають силою зростання. Формула нарощення по безупинної відсоткової ставки має вигляд

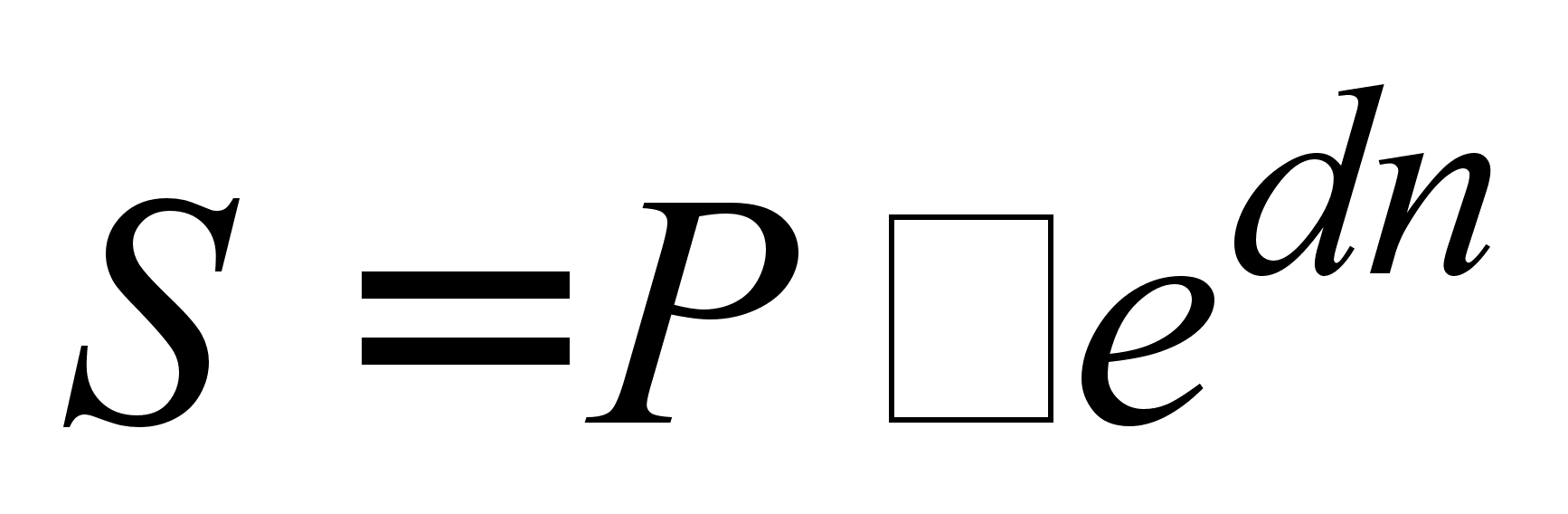, (2.1.19)

де e - основа натурального логарифма (≈ 2,71828 ...); edn - множник нарощення безперервних відсотків.

Наприклад, на скільки зросте через три роки сума 250 тис. Руб., Якщо сьогодні покласти її на банківський депозит під 15% річних, що нараховуються безперервно?

S = 250  e ^ (0,15  3) = 392,1 тис. Руб.

Для безперервних відсотків не існує відмінностей між процентною і облікової ставками, оскільки сила зростання - універсальний показник. Однак поряд з постійною силою зростання може використовуватися змінна процентна ставка, величина якої змінюється по заданому закону (математичної функції). В цьому випадку можна будувати дуже потужні імітаційні моделі, однак математичний апарат розрахунку таких моделей досить складний і не розглядається в цьому посібнику, так само як і нарахування відсотків по змінної безперервної процентній ставці.

Безперервне дисконтування з використанням постійної сили зростання виконується за формулою

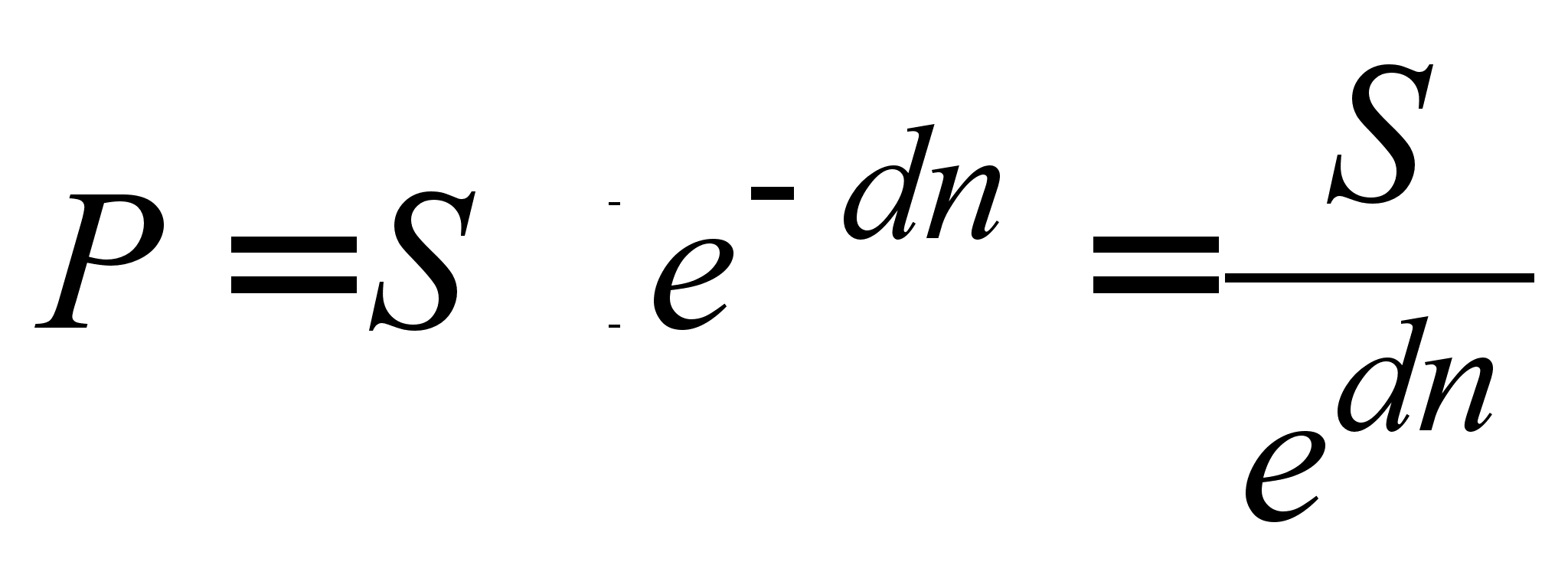, (2.1.20)

де 1 / edn - дисконтний множник дисконтування за силою росту.

Наприклад, в результаті здійснення інвестиційного проекту планується отримати через два роки дохід у розмірі 15 млн. Руб. Чому буде дорівнювати приведена вартість цих грошей в сьогоднішніх умовах, якщо сила зростання становить 22% річних?

P = 15 / e ^ (0,22  2) = 9,66 млн. Руб.

розділ: різне
Кількість знаків з пробілами: 221 679
Кількість таблиць: 15
Кількість зображень: 131

... Федерації і постанови Уряду Російської Федерації. Прийняття нормативних правових актів зазначеного органу має здійснюватися на підставі рішення колегіального органу, що здійснює регулювання фінансового ринку. Передбачається, що члени колегіального органу матимуть статус державних службовців і призначатися Урядом Російської Федерації на певний термін і ...

... 7. Складаються на підприємстві плани збалансовані між собою. Таким чином, тільки в результаті реалізації цих функцій на практиці можна говорити про постановку і організації фінансового планування на підприємстві. Що стосується аналізованої організації ЗАТ «Центр» для побудови ефективної системи фінансового планування важливо визначити не тільки функції, але і методи планування. ...

... І. Т. Основи фінансового менеджменту. Як управляти капіталом? - М .: Фінанси і статистика, 1995. - 384 с. 2. Дибаль С. В. Фінансовий аналіз теорія і практика: Учеб. посібник. - СПб .: Видавничий дім "Бізнес-преса", 2004. - 304 с. 3. В. В. Ковальов, О. М. Волкова "Аналіз господарської діяльності підприємства"; Москва, - Проспект, 2004.. - стор. 240-256; 4. В. В. Ковальов. Введення у фінансовий ...

... отримання доходів у повному обсязі), залежить від безлічі факторів, що впливають на підприємство зсередини і ззовні. У цій ситуації і проявляється поняття ризику. Операційний важіль (або операційний леверидж) - це механізм управління операційним прибутком, заснований на поділі всієї сукупності операційних витрат підприємства на постійні та змінні. Дія або ефект операційного важеля ...