1. Питання проектування електричних кабелів
2. Результати аналітичного рішення для коаксіальногокабелю
3. Моделювання кабелів в модулі AC / DC
4. Розподілені параметри для шунтирующей провідності і ємності
5. Питомі параметри для послідовного опору і індуктивності
6. Характеристичний імпеданс і постійна поширення
7. Моделювання кабелю в області високих частот
8. Модальний аналіз в модулі Радіочастоти і модулі Хвильова оптика
9. Заключні зауваження по моделюванню кабелів
10. література

Електричні кабелі характеризуються такими параметрами, як імпеданс і коефіцієнт загасання. В даному топіку буде розглянуто приклад моделювання коаксіальногокабелю, для якого існує аналітичне рішення. Ми покажемо вам, як розрахувати параметри кабелю, виходячи з результатів моделювання електромагнітних полів в середовищі COMSOL Multiphysics. Розібравшись з принципами побудови моделі коаксіальногокабелю, в подальшому ми зможемо застосовувати отримані знання для обчислення параметрів ліній передач або кабелів довільного типу.

Питання проектування електричних кабелів

Електричні кабелі, звані також лініями електропередачі, в даний час повсюдно застосовуються для передачі даних і електроенергії. Навіть якщо ви читаєте цей текст з екрана на стільникового телефону або планшетного комп'ютера, використовуючи "бездротову" зв'язок, все одно всередині вашого пристрою залишаються "провідні" лінії електропередачі, що з'єднують різні електричні компоненти в єдине ціле. А повернувшись ввечері додому, ви, швидше за все, підключіть до пристрою кабель живлення для зарядки.

Застосовуються найрізноманітніші лінії електропередач від малих, виконаних у вигляді копланарних волноводов на друкованих монтажних платах, до дуже великих високовольтних ліній електропередачі . Вони також повинні функціонувати в різних і, найчастіше, екстремальних режимах і умовах експлуатації, від трансатлантичних телеграфних кабелів до електропроводки на космічних кораблях, зовнішній вигляд якої наведено на малюнку нижче. Лінії передачі необхідно розробляти з урахуванням всіх необхідних вимог, щоб гарантувати їх надійну роботу в заданих умовах. Крім цього, вони можуть бути предметом досліджень з метою подальшої оптимізації конструкції, включно з виконанням вимог по механічної міцності і малій вазі.

З'єднувальні дроти в вантажному відсіку макета шаттла OV-095 в Shuttle Avionics Integration Laboratory (SAIL).

При проектуванні і використанні кабелів, інженери часто оперують з розподіленими (або питомими, тобто припадають на одиницю довжини) параметрами для послідовного опору (R), послідовної індуктивності (L), шунтирующей ємності (C), і шунтирующей провідності (G, іноді званої провідність ізоляції). Ці параметри цілком можна використовувати для розрахунку якості функціонування кабелю, його характеристичного імпедансу і втрат в ньому при поширенні сигналів. Однак важливо мати на увазі, що ці параметри знаходяться з рішення рівнянь Максвелла для електромагнітного поля. Для чисельного рішення рівнянь Максвелла з метою розрахунку електромагнітних полів, а також для обліку впливу мультіфізіческіх ефектів, можна використовувати середу COMSOL Multiphysics, що дозволить визначити, яким чином змінюються параметри кабелю і його ефективність при різних режимах роботи та умови експлуатації. Розроблена модель може бути згодом перетворена в інтуїтивно-зрозумілий додаток, подібно до наведеного в даному прикладі , Яке розраховує параметри для стандартних і часто використовуваних ліній передач.

В даному топіку ми розберемо випадок коаксіальногокабелю - фундаментального завдання, яка зазвичай міститься в будь-якому стандартному навчальному курсі з СВЧ-техніці або лініях електропередач. Коаксіальний кабель є настільки фундаментальним фізичним об'єктом, що Олівер Хевісайд (Oliver Heaviside) запатентував його в 1880 році, через всього лише кілька років після того, як Максвелл сформулював свої знамениті рівняння. Для студентів, які вивчають історію науки - це той самий Олівер Хевісайд, який вперше сформулював рівняння Максвелла в тому векторному вигляді, який є тепер загальноприйнятим; той, хто вперше використав термін "імпеданс"; і хто вніс вагомий внесок в розвиток теорії ліній електропередач.

Результати аналітичного рішення для коаксіальногокабелю

Почнемо своє розгляд з коаксіальногокабелю, що має характерні розміри, позначені на схематичному зображенні його поперечного перерізу, представленому нижче. Діелектрична серцевина між внутрішнім і зовнішнім провідником має відносну діелектричну проникність (\ epsilon_r = \ epsilon '-j \ epsilon' ') дорівнює 2.25 - j * 0.01, відносну магнітну проникність (\ mu_r) рівну 1 і нульову провідність, тоді як внутрішній і зовнішній провідники мають провідність (\ sigma) рівною 5.98e7 С / м (Сіменс / метр).

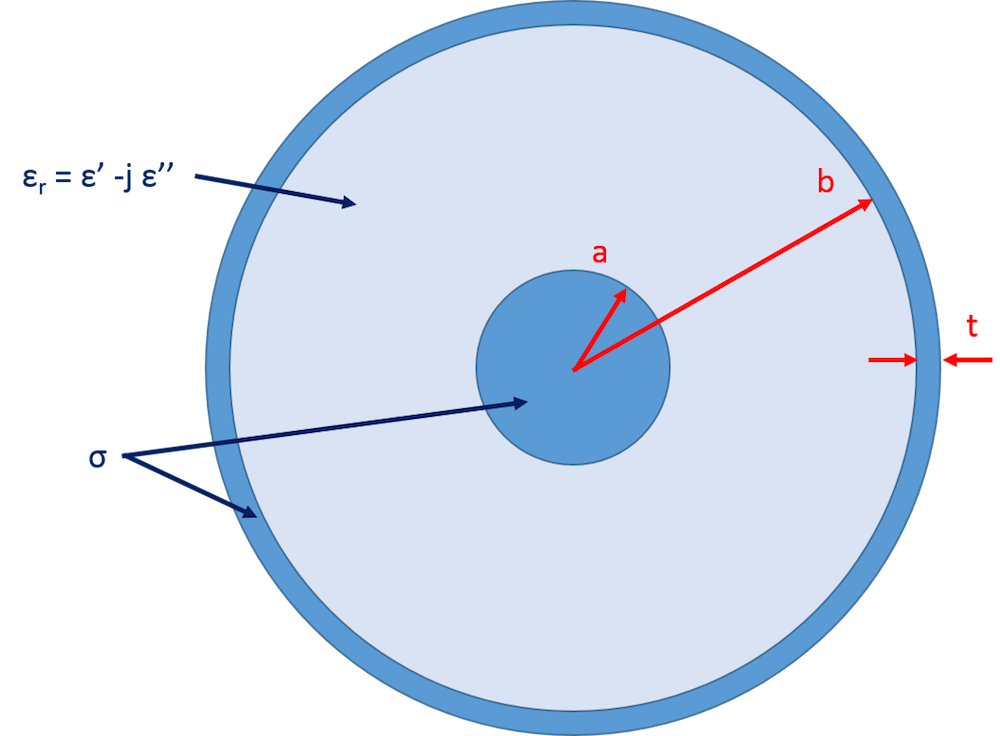
2D поперечний переріз коаксіальногокабелю зі значеннями характерних розмірів: a = 0.405 мм, b = 1.45 мм, і t = 0.1 мм.

Стандартний метод вирішення для ліній електропередач полягає в тому, що структура електромагнітних полів в кабелі передбачається відомої, а саме вважається, що вони будуть осциллировать і затухати в напрямку поширення хвилі, в той час як в поперечному напрямку профіль перетину поля залишається незмінним. Якщо потім ми знаходимо рішення, яке задовольняє вихідним рівнянням, то в силу теореми єдиності, знайдене рішення буде вірним.

На математичній мові все вищесказане еквівалентно тому, що рішення рівнянь Максвелла шукається у вигляді анзаців -форми

для електромагнітного поля \ mathbf {E} \ left (x, y, z \ right) = \ mathbf {\ tilde {E}} \ left (x, y \ right) e ^ {- \ gamma z}, де (\ gamma = \ alpha + j \ beta) є комплексною постійної поширення, а \ alpha і \ beta є коефіцієнтами загасання і поширення, відповідно. В циліндричних координатах для коаксіального кабелю, це призводить до добре відомим рішенням для полів

\ Begin {align}
\ Mathbf {E} & = \ frac {V_0 \ hat {r}} {rln (b / a)} e ^ {- \ gamma z} \\
\ Mathbf {H} & = \ frac {I_0 \ hat {\ phi}} {2 \ pi r} e ^ {- \ gamma z}
\ End {align}

з яких потім виходять розподілені параметри на одиницю довжини

\ Begin {align}
L & = \ frac {\ mu_0 \ mu_r} {2 \ pi} ln \ frac {b} {a} + \ frac {\ mu_0 \ mu_r \ delta} {4 \ pi} (\ frac {1} {a} + \ frac {1} {b}) \\
C & = \ frac {2 \ pi \ epsilon_0 \ epsilon '} {ln (b / a)} \\
R & = \ frac {R_s} {2 \ pi} (\ frac {1} {a} + \ frac {1} {b}) \\
G & = \ frac {2 \ pi \ omega \ epsilon_0 \ epsilon ''} {ln (b / a)}
\ End {align}

де R_s = 1 / \ sigma \ delta - поверхневий опір, а \ delta = \ sqrt {2 / \ mu_0 \ mu_r \ omega \ sigma} є глибиною скін-шару .

Надзвичайно важливо підкреслити, що співвідношення для ємності і шунтирующей провідності виконуються для будь-яких частот, в той час як вираження для опору і індуктивності залежать від глибини скін-шару і, отже, можуть бути застосовані лише при частотах, на яких глибина скін-шару багато менше фізичної товщини провідника. Саме тому другий член у виразі для індуктивності, званий також внутрішньої індуктивністю, може бути незнайомий деяким читачам, так як їм зазвичай нехтують, коли метал розглядається як ідеальний провідник. Цей член являє собою індуктивність, викликану проникненням магнітного поля в метал, що володіє кінцевою провідністю, і дуже малий при досить високих частотах. (Він також може бути представлений у вигляді L_ {Internal} = R / \ omega.)

Для подальшого зіставлення з чисельними результатами, можна обчислити співвідношення для опору по постійному струму з виразу для провідності і площі поперечного перерізу металу. Аналітичний вираз для індуктивності (по постійному струму) трохи складніше, і тому ми наводимо його тут для довідки.

L_ {DC} = \ frac {\ mu} {2 \ pi} \ left \ {ln \ left (\ frac {b + t} {a} \ right) + \ frac {2 \ left (\ frac {b} {a} \ right) ^ 2} {1 \ left (\ frac {b} {a} \ right) ^ 2} ln \ left (\ frac {b + t} {b} \ right) - \ frac { 3} {4} + \ frac {\ frac {\ left (b + t \ right) ^ 4} {4} - \ left (b + t \ right) ^ 2a ^ 2 + a ^ 4 \ left (\ frac {3} {4} + ln \ frac {\ left (b + t \ right)} {a} \ right)} {\ left (\ left (b + t \ right) ^ 2-a ^ 2 \ right) ^ 2} \ right \}

Тепер, коли у нас є значення C і G у всьому діапазоні частот, значення для R і L за постійним струмом, і їх асимптотичні значення в області високих частот, ми володіємо прекрасними орієнтирами для порівняння з чисельними результатами.

Моделювання кабелів в модулі AC / DC

При постановці завдання для чисельного моделювання, завжди важливо враховувати наступний момент: чи можливе використання симетрії завдання для зменшення розмірів моделі і збільшення швидкості обчислень. Як ми бачили раніше, точне рішення буде мати вигляд \ mathbf {E} \ left (x, y, z \ right) = \ mathbf {\ tilde {E}} \ left (x, y \ right) e ^ {- \ gamma z}. Оскільки нас цікавить просторове зміна полів, відбувається в першу чергу в xy -плоскості, то ми хочемо виконати моделювання тільки в 2D-поперечному перерізі кабелю. Однак при цьому виникає проблема, яка полягає в тому, що для 2D-рівнянь, які використовуються в AC / DC модулі, передбачається, що поля залишаються інваріантними в напрямку перпендикулярному площині моделювання. Це означає, що ми не зможемо отримати інформацію про просторове зміні анзаців-рішення за рахунок єдиного 2D AC / DC-моделювання. Однак за допомогою моделювання в двох різних площинах це можливо. Послідовний опір і індуктивність залежать від струму і енергії, запасеної в магнітному полі, тоді як шунтирующая провідність і ємність залежать від енергії в електричному полі. Розглянемо ці аспекти більш докладно.

Розподілені параметри для шунтирующей провідності і ємності

Оскільки шунтирующая провідність і ємність можуть бути розраховані, виходячи з розподілу електричного поля, почнемо з застосування інтерфейсу Електричні струми.

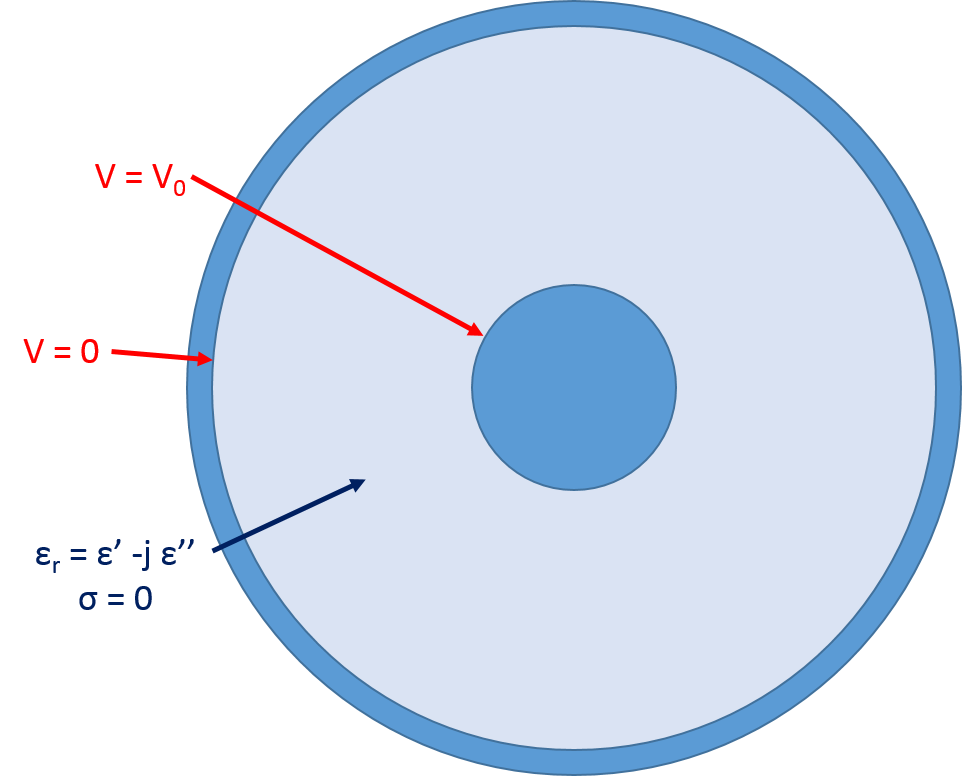
Граничні умови і властивості матеріалу для інтерфейсу моделювання Електричні струми.

Після того, як геометрія моделі визначена і привласнені значення властивостям матеріалу, робиться припущення про те, що поверхня провідників є еквіпотенційної (що абсолютно обгрунтовано, оскільки різниця в провідності між провідником і діелектриком, становить, як правило, майже 20 порядків за величиною). Потім ми задаємо значення фізичних параметрів, привласнюючи внутрішнього провідника електричний потенціал V0 і заземлення зовнішньому провіднику для знаходження електричного потенціалу в діелектрику. Вищевказані аналітичні вирази для ємності виходять з наступних найбільш загальних співвідношень

\ Begin {align}
W_e & = \ frac {1} {4} \ int_ {S} {} \ mathbf {E} \ cdot \ mathbf {D ^ \ ast} d \ mathbf {S} \\
W_e & = \ frac {C | V_0 | ^ 2} {4} \\
C & = \ frac {1} {| V_0 | ^ 2} \ int_ {S} {} \ mathbf {E} \ cdot \ mathbf {D ^ \ ast} d \ mathbf {S}
\ End {align}

де перше співвідношення є рівнянням електромагнітної теорії, а друге рівнянням теорії ланцюгів.

Третє співвідношення є комбінацією першого і другого рівнянь. Підставляючи вищевказані відомі вирази для полів, ми отримаємо наведений раніше аналітичний результат для C в коаксіальному кабелі. У підсумку ці рівняння дозволяють нам визначити ємність через значення полів для довільного кабелю. За результатами моделювання, ми можемо обчислити інтеграл щільності електричної енергії, що дає для ємності значення 98.142 пФ / м і збігається з теорією. Оскільки G і C і пов'язані виразом

G = \ frac {\ omega \ epsilon '' C} {\ epsilon '}

у нас тепер є два з чотирьох параметрів.

Варто повторити, що ми зробили припущення про те, що провідність діелектричної області дорівнює нулю. Це стандартне припущення, яке робиться у всіх навчальних посібниках, і ми також дотримуємося тут цією угодою, тому що воно не робить істотного впливу на фізику - на відміну від включення нами в розгляд члена внутрішньої індуктивності, що обговорювалося раніше. Багато матеріалів для діелектричного сердечника мають ненульовий провідність, але це легко може бути враховано при моделюванні, просто підставивши нові значення в властивості матеріалу. В цьому випадку, для забезпечення належного зіставлення з теорією, необхідно також внести відповідні поправки в теоретичні вирази.

Питомі параметри для послідовного опору і індуктивності

Аналогічним чином, послідовний опір і індуктивність можна розрахувати за допомогою моделювання при використанні інтерфейсу Магнітні поля в модулі AC / DC. Налаштування моделювання елементарні, що ілюструється на малюнку нижче.

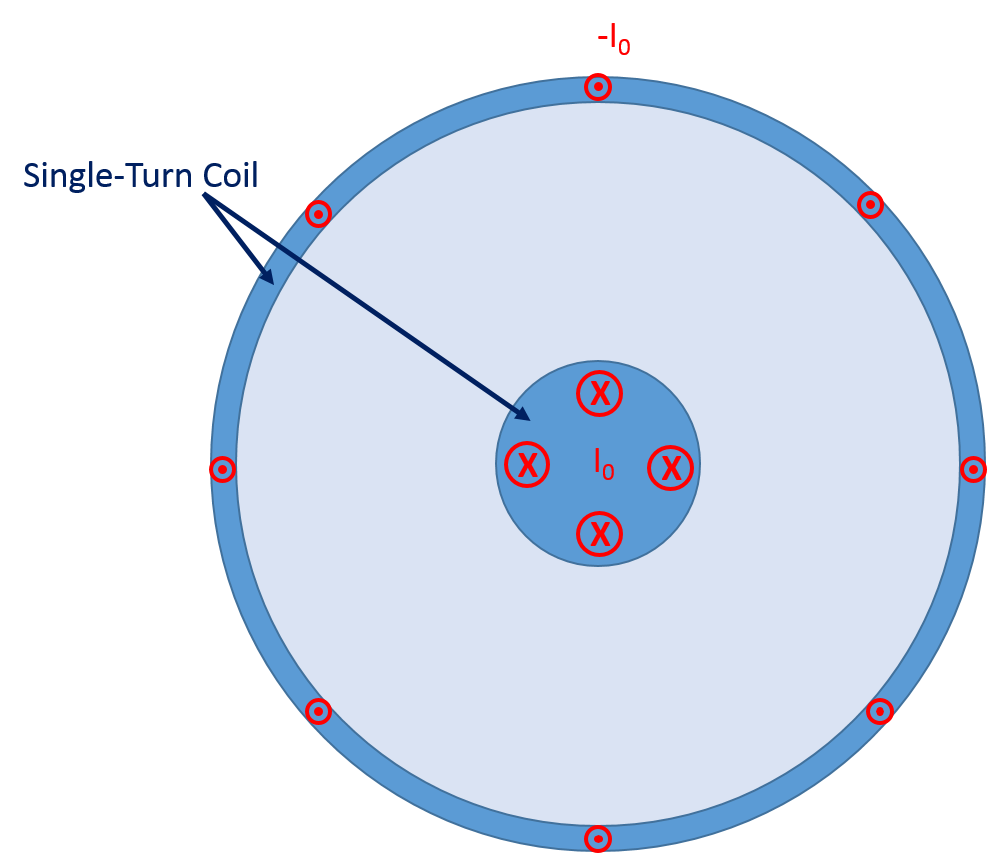
Області провідників додаються до вузла одновиткового Котушка в розділі Група котушок, і, обрана опція зворотного напрямку струму гарантує, що напрямок струму у внутрішньому провіднику буде протилежним току зовнішнього провідника, що позначається на малюнку точками і хрестиками. При розрахунку частотної залежності буде враховуватися розподіл струму в одновітковой котушці, а не довільний розподіл струму, показане на малюнку.

Для обчислення індуктивності звернемося до наступних рівнянь, які є магнітним аналогом попередніх рівнянь.

\ Begin {align}
W_m & = \ frac {1} {4} \ int_ {S} {} \ mathbf {B} \ cdot \ mathbf {H ^ \ ast} d \ mathbf {S} \\
W_m & = \ frac {L | I_0 | ^ 2} {4} \\
L & = \ frac {1} {| I_0 | ^ 2} \ int_ {S} {} \ mathbf {B} \ cdot \ mathbf {H ^ \ ast} d \ mathbf {S}
\ End {align}

Для обчислення опору, застосовується дещо інша техніка. Перш за все, ми інтегруємо резистивні втрати для визначення потужності, що розсіюється, що припадає на одиницю довжини. А потім використовуємо добре відоме співвідношення P = I_0 ^ 2R / 2 для розрахунку опору. Оскільки R і L змінюються з частотою, давайте подивимося на розрахункові значення і аналітичне рішення в межі постійного струму і в області високих частот.

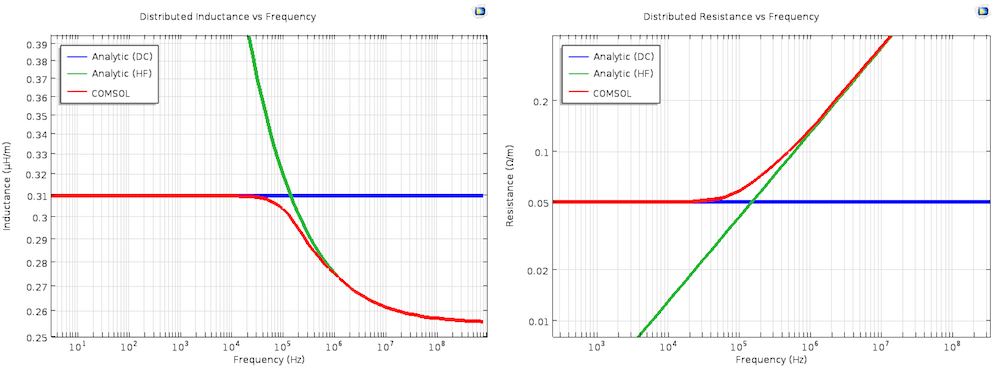
"Аналітичне рішення для постійного струму" і "Аналітичне рішення в області високих частот" графічні залежності відповідають рішенням аналітичних рівнянь для постійного струму і в області високих частот, які обговорювалися раніше в тексті статті. Відзначимо, що обидві залежності наведені в логарифмічному масштабі по частотної осі.

Добре видно, що розрахункові значення плавно переходять з рішення для постійного струму в області низьких частот в високочастотне рішення, яке буде справедливим при глибині скін-шару багато меншої товщини провідника. Розумно припустити, що перехідна область розташовується приблизно в тому місці по осі частот, де глибина скін-шару і товщина провідника розрізняються не більше ніж на порядок величини. Ця область лежить в діапазоні від 4.2e3 Гц до 4.2e7 Гц, що в точності відповідає очікуваному результату.

Характеристичний імпеданс і постійна поширення

Тепер, коли ми завершили трудомістку роботу з обчислення R, L, C, і G, залишаються ще два інших, істотних для аналізу ліній електропередач параметра, які потрібно визначити. Ними є характеристичний імпеданс (Zc) і комплексна постійна поширення (\ gamma = \ alpha + j \ beta), де \ alpha - коефіцієнт загасання, а \ beta - коефіцієнт поширення.

\ Begin {align}
Z_c & = \ sqrt {\ frac {(R + j \ omega L)} {(G + j \ omega C)}} \\
\ Gamma & = \ sqrt {(R + j \ omega L) (G + j \ omega C)}
\ End {align}

На малюнку нижче, представлені ці значення, обчислені за допомогою аналітичних формул в режимах постійного струму і високочастотного сигналу, в порівнянні зі значеннями, визначеними за результатами моделювання. Крім цього, четвертої залежністю на графіку є імпеданс, розрахований в середовищі COMSOL Multiphysics за допомогою модуля Радіочастоти, який ми коротко розглянемо трохи пізніше. Як можна помітити, результати чисельного моделювання добре узгоджуються з аналітичними рішеннями для відповідних граничних режимів, а також дають правильні значення в перехідній області.

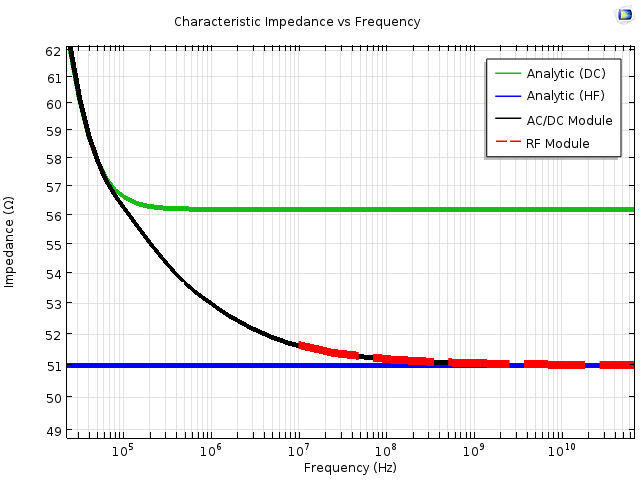
Порівняння характеристичного імпедансу, обчисленого з використанням аналітичних виразів і визначеного за результатами моделювання в середовищі COMSOL Multiphysics. Аналітичні криві будувалися за допомогою відповідних граничних виразів для режиму постійного струму і високочастотної області, розглянутих раніше, тоді як для моделювання в середовищі COMSOL Multiphysics використовувалися модулі AC / DC і Радіочастоти. Для наочності, товщина лінії "RF module" була спеціально збільшена.

Моделювання кабелю в області високих частот

Енергія електромагнітного поля поширюється у вигляді хвиль, а значить робоча частота і довжина хвилі обернено пропорційні один одному. У міру того, як ми зрушуємося в область все більш високих частот, ми змушені брати до уваги відносний розмір довжини хвилі і електричний розмір кабелю. Як обговорювалося в попереднього запису , Ми повинні змінити AC / DC на модуль Радіочастоти при електричному розмірі приблизно λ / 100 (про концепцію «електричного розміру» см. Там же). Якщо в якості електричного розміру ми виберемо діаметр кабелю, а замість швидкості світла у вакуумі - швидкість світла в діелектричному осерді кабелю, то отримаємо частоту для переходу в районі 690 МГц.

При таких високих частотах, сам кабель більш доречно розглядати в якості хвилеводу, а збудження кабелю можна розглядати, як моди хвилеводу. Використовуючи хвилевідну термінологію, до сих пір ми розглядали моду спеціального типу, звану TEM -модем, яка може поширюватися на будь-якій частоті. Коли поперечний переріз кабелю та довжина хвилі стають порівнянні, ми також повинні враховувати можливість існування мод вищих порядків. На відміну від TEM-моди більшість хвилеводних мод може поширюватися тільки при частоті збудження вище деякої характеристичної частоти відсічення. Завдяки циліндричної симетрії в нашому прикладі, є вираз для частоти відсічення першої моди вищого порядку - TE11. Ця частота відсічення fc = 35.3 ГГц, але навіть при такій відносно простий геометрії, частота відсічення є рішенням трансцендентного рівняння, яке ми не будемо розглядати в даній статті.

Так Пожалуйста значення для наших результатів має ця сама частота відсічення? Вище цієї частоти, енергія хвилі, що переноситься в TEM-моді, якої ми цікавимося, має потенційну можливість вступити у взаємодію з TE11-модою. У ідеалізованої геометрії, подібної змодельованої тут, ніякого взаємодії не буде. У реальному ж ситуації, однак, будь-які дефекти в конструкції кабелю можуть привести до взаємодії мод на частотах вище частоти відсічення. Це може бути результатом впливу цілого ряду неконтрольованих чинників: від похибок виготовлення до градієнтів властивостей матеріалу. Таку ситуацію найпростіше уникнути на стадії проектування кабелів, розрахований роботу на свідомо більш низьких частотах, ніж частота відсічення мод вищого порядку, так щоб поширюватися могла тільки одна мода. Якщо це становить інтерес, то ви можете також використовувати середу COMSOL Multiphysics для моделювання взаємодії між модами вищих порядків, як це зроблено в цій навчальної моделі Направленого ответвителя (Хоча це виходить за рамки цієї статті).

Модальний аналіз в модулі Радіочастоти і модулі Хвильова оптика

Моделювання мод вищих порядків ідеально реалізується за допомогою модального аналізу в модулі Радіочастоти і модулі Хвильова оптика. Анзаців-формою рішення в цьому випадку є вираз \ mathbf {E} \ left (x, y, z \ right) = \ mathbf {\ tilde {E}} \ left (x, y \ right) e ^ {- \ gamma z}, яке в точності відповідає структурі мод, що і є нашою метою. В результаті, модальний аналіз відразу видає рішення для просторового розподілу поля і комплексної постійної поширення для кожної з заданої кількості мод. При цьому ми можемо використовувати ту ж геометрію моделі, що й колись, за винятком того, що нам достатньо використовувати в якості області моделювання тільки діелектричний сердечник і граничні умови імпеданс для металевих провідників .

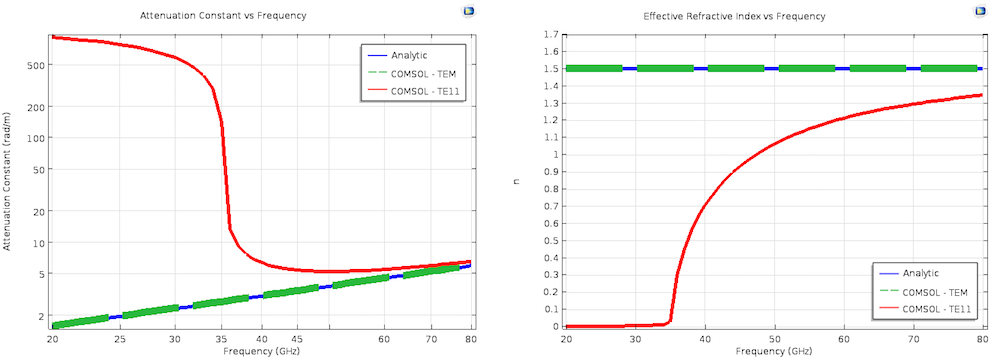
Результати розрахунку константи загасання і ефективного показника заломлення хвильової моди з модів Аналізу. Аналітична крива на лівому графіку - коефіцієнт загасання в залежності від частоти - обчислюється з використанням тих же самих виразів, як і в разі ВЧ-кривих, використовуваних для порівняння з результатами моделювання в AC / DC модулі. Аналітична крива на правому графіку - ефективний показник заломлення в залежності від частоти - це просто n = \ sqrt {\ epsilon_r \ mu_r}. Для наочності, розмір лінії "COMSOL - TEM" був навмисно збільшений на обох графіках.

Чітко видно, що результати модовая Аналізу TEM-моди збігаються з аналітичної теорією і, що розрахована мода вищого порядку з'являється на попередньо певній частоті відсічення. Зручно, що комплексна постійна поширення безпосередньо обчислюється в процесі моделювання і не вимагає проміжних обчислень R, L, C, і G. Це стає можливим в силу того, що \ gamma явно включена в шукану форму анзаців-рішення і знаходиться при вирішенні підстановкою її в основне рівняння. При бажанні, інші параметри також можуть бути обчислені для TEM-моди, а більш детальну інформацію про це можна знайти в цієї демонстраційної моделі з Галереї Додатків. Заслуговує також на увагу той факт, що цей же метод модального аналізу може бути використаний для розрахунку діелектричних хвилеводів, як це реалізовано в волоконної оптики .

Заключні зауваження по моделюванню кабелів

До теперішнього моменту ми ретельно проаналізували модель коаксіальногокабелю. Ми вирахували розподілені параметри від режиму постійного струму до області високих частот і розглянули першу моду вищого порядку. Важливо, що результати модального аналізу залежать тільки від геометричних розмірів і властивостей матеріалу кабелю. Результати для моделювання в модулі AC / DC вимагають додаткової інформації про те, яким чином кабель збуджується, але, сподіваюся, ви в курсі про те, що підключається до вашого кабелю! Ми використовували аналітичну теорію виключно для того, щоб порівняти результати чисельного моделювання з добре відомими результатами для еталонної моделі. Це означає, що аналіз можна узагальнити і на інші кабелі, так само як і додати до нього взаємозв'язку для мультіфізіческого моделювання, які включають в себе температурні зміни і структурні деформації.

Кілька цікавих нюансів для побудови моделі (у вигляді відповідей на можливі запитання):

• "Чому ви не згадали і / або не привели графіки характеристичного імпедансу і всіх розподілених параметрів для TE11-моди?"
  • Тому що тільки TEM-моди мають однозначно визначені напруга, струм і характеристичний імпеданс. В принципі, можливо, приписати деякі з цих значень модам вищих порядків, і це питання більш детально буден розглянуто в подальших статтях, а також у різних роботах по теорії ліній передач і СВЧ-техніки.
• "Коли я вирішую завдання на моди з використанням модальності аналізу, вони маркуються за допомогою своїх робочих індексів. Звідки беруться позначення TEM- і TE11-мод? "
  • Ці позначення з'являються при теоретичному аналізі і використовуються для зручності при обговоренні результатів. Таке найменування не завжди можливо при довільній геометрії хвилеводу (або кабелю в волноводном режимі), проте варто враховувати, що дане позначення всього лише "ім'я". Яке б найменування не було у моди, вона як і раніше несе електромагнітну енергію (крім, зрозуміло, нетуннелірующіе еванесцентні хвилі)?
• "Чому в деяких ваших формулах присутній додатковий множник ½?"
  • Це відбувається при вирішенні задач електродинаміки в частотної області, а саме, при множенні двох комплексних величин. При виконанні усереднення за часом, з'являється додатковий множник ½, на відміну від виразів в тимчасовій області (або при постійному струмі). За додатковою інформацією ви можете звернутися до праць по класичній електродинаміки.

література

Наступні монографії були використані при написанні цієї замітки і послужать чудовими джерелами при пошуку додаткової інформації:

• Microwave Engineering (СВЧ техніка), by David M. Pozar
• Foundations for Microwave Engineering (Основи СВЧ-техніки), by Robert E. Collin
• Inductance Calculations (Розрахунок індуктивності), by Frederick W. Grover
• Classical Electrodynamics (Класична електродинаміка), by John D. Jackson