1. Реклама

Булевої алгебри (булева решітка), частково впорядкована множина спеціального виду. Булеву алгебру можна формально визначити як непорожня множина з операціями V, Λ,?, Що задовольняють аксіомам:

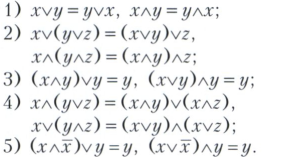
Впорядкування елементів Булевой алгебри вводиться умовою: ху точно тоді, коли х = хΛу. У Булевой алгебрі існує найбільший елемент 1 - одиниця Булевої алгебри, 1 = xvx ?, �� найменший елемент 0 - нуль булевої алгебри, 0 = хΛx ?. Операції v і Λ називаються диз'юнкція і кон'юнкція і іноді позначаються sup і inf, ніж підкреслюється їх схожість з теоретико-множинними операціями об'єднання і перетину. Кон'юнкція також позначається символом &. Елемент Булевой алгебри x? називається доповненням х і іноді позначається Сх, х ', х, х. Доповнення всякого елемента в Булевой алгебри єдино.

Булеву алгебру можна визначити і як дистрибутивну грати (дистрибутивну структуру; дивись решіток теорія), що має найбільший елемент 1 - одиницю Булевой алгебри, найменший елемент 0 - нуль Булевой алгебри і містить разом з кожним своїм елементом х його доповнення - елемент Сх, що задовольняє співвідношенням

Реклама

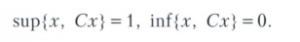
Можливі й інші аксіоматичні визначення Булевой алгебри. В аксіомах Булевой алгебри відображена аналогія між поняттями безлічі, події, висловлювання. Ставлення порядку в Булевой алгебри може бути (в залежності від вибору інтерпретації) витлумачено як теоретико-множинне включення, як причинне проходження для подій, як логічне слідування для висловлювань.

Крім основних операцій V, Λ,?, В Булевой алгебри можуть бути визначені й інші, серед яких особливо важлива операція симетричної різниці

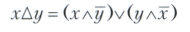
(Пишуть також х +2 у, | х-у |).

Булеві алгебри були введені Дж. Булем (1847) як апарат символічної логіки. В подальшому Булеві алгебри знайшли широке застосування в різних розділах математики - в теорії ймовірностей, топології, функціональному аналізі та ін. В основі додатків Булевой алгебри до логіки лежить інтерпретація елементів Булевой алгебри як висловлювань (дивись Алгебра логіки); при цьому додаток Сх тлумачиться як заперечення висловлювання х, а операції Λ і v - як кон'юнкція і диз'юнкція висловлювань. До логіки близька і інша область застосування Булевой алгебри - теорія контактних схем. Булеві алгебри використовуються в аксіоматиці теорії ймовірностей. Алгебри подій, що вивчаються в теорії ймовірностей, суть Булевой алгебри; при цьому нерівність х ≤ у означає, що подія х тягне подія у, відповідно з цим тлумачаться нуль Булевой алгебри, одиниця Булевой алгебри і булеві операції V, Λ,?.

Прикладом Булевой алгебри є упорядкована по включенню система всіх підмножин фіксованого безлічі Q. Така Булева алгебра позначається 2Q; її нулем служить порожня множина, одиницею - саме безліч Q. Доповнення елемента х є безліч Qх; булеві операції v і Λ збігаються відповідно з об'єднанням і перетином.

Будь-яка Булева алгебра Х ізоморфна деякій алгебрі множин. Булева алгебра Х називається повною, якщо будь-яке безліч Е з Х має верхню грань sup Е і нижню межу inf Е. Неповна Булева алгебра може бути багатьма способами поповнена, т. е. вкладена в якості подалгебри в деяку повну Булеву алгебру.

Повна Булева алгебра називається нормованою, якщо на ній визначена дійсна функція μ (міра), що володіє властивостями: μ (х)> 0 при Х ≠ 0; якщо ЕСХ і хΛу = 0 при х, уЄЕ, х ≠ у, то

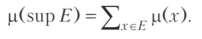
У теорії ймовірностей, де нормовані Булеві алгебри особливо важливі, зазвичай припускають, що μ (1) = 1. При цьому значення μ (х) інтерпретується як імовірність події Х. На нормовані Булеві алгебри в основному переноситься класична теорія міри та інтеграла. Не всяка Булева алгебра може бути нормована. Відомі різні умови існування заходи, проте вони далеко не вичерпують проблеми нормованої.

Булева алгебра може бути наділена різними топологиями. Особливо важлива так звана (о) -топологія, яка в разі нормованої Булевой алгебри метрізуемості і відповідає метриці

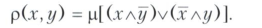
У загальному випадку може не існувати топології, гармонійно поєднаною з порядком в булевої алгебри.

Літ .: Boole G. The mathematical analysis of logic. Camb .; L. 1847; Біркгоф Г. Теорія структур. М., 1952; Halmos Р. Lectures on Boolean algebras. Toronto а. о., 1963; Kypamoвскій К. Топологія. М., 1969. Т. 2; Сікорський Р. Булеві алгебри. М., 1969; Владимиров Д. А. Булеві алгебри. М., 1969; Расева Е., Сікорський Р. Математика метаматематики. М., 1972.

Д. А. Владимиров.